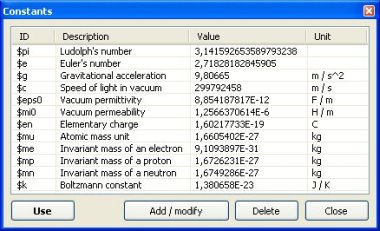
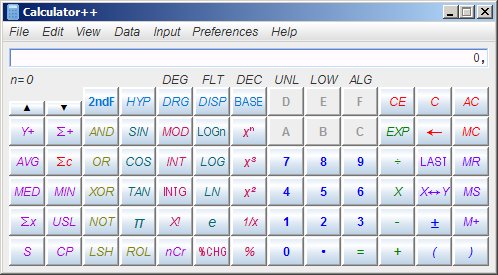
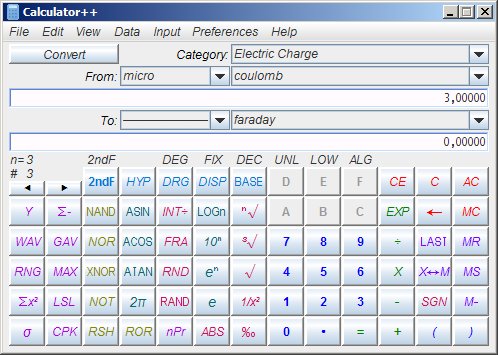
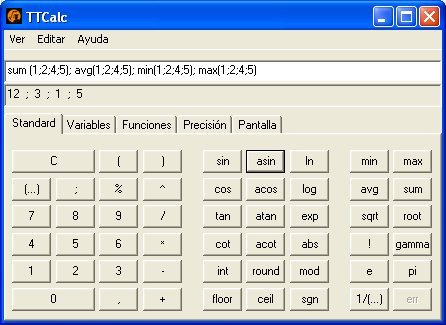
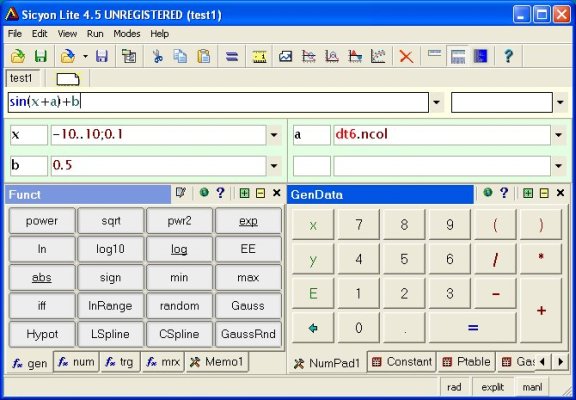
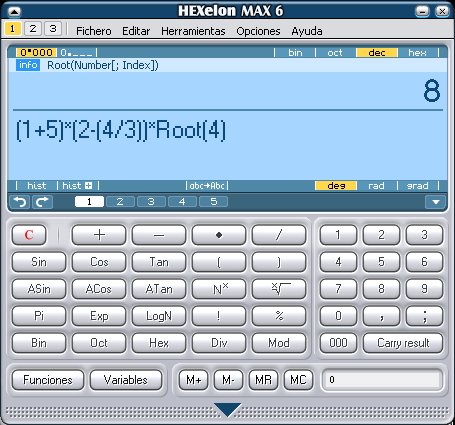
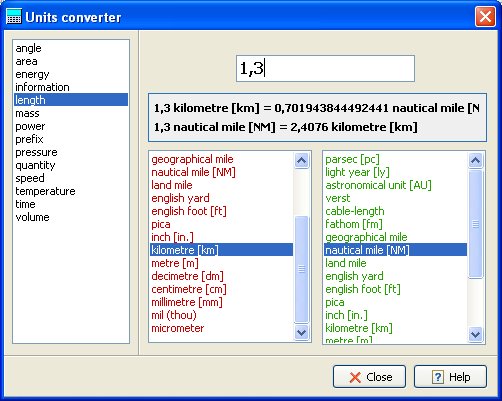
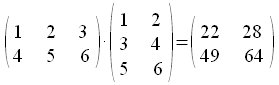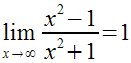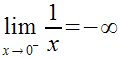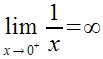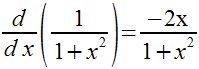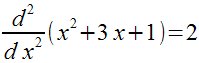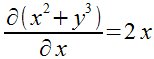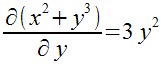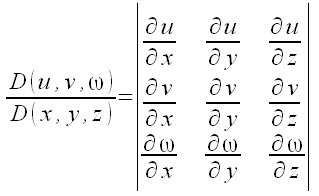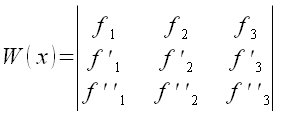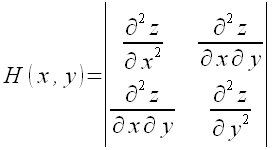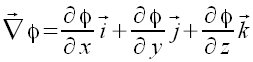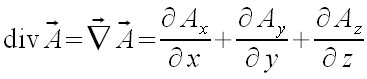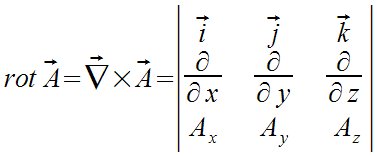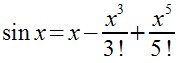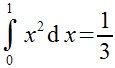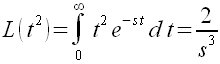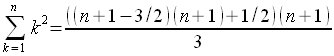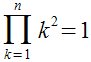De momento no hemos incluido conversores de unidades,
pues alguna de las calculadoras analizadas ya incluyen un conversor entre
diferentes tipos de medidas.
No hemos analizado otros programas más complejos
(con un tamaño de programa mucho mayor) como: Maxima [http://maxima.sourceforge.net/es/]
(cuya última versión, 5.27.0.1 ocupa 31,8 MB), Euler Math
Toolbox [http://eumat.sourceforge.net/]
(cuya última versión, 22 ocupa 82 MB), Octave [http://octave.sourceforge.net/]
(su última versión 3.2.4 ocupa 71,3 MB) o Scilab [http://www.scilab.org/]
(cuya última versión, 5.3.3 ocupa 122 MB). Tampoco hemos
analizado programas comerciales como Derive, Mathcad, MatLab, Mathematica
o Maple.
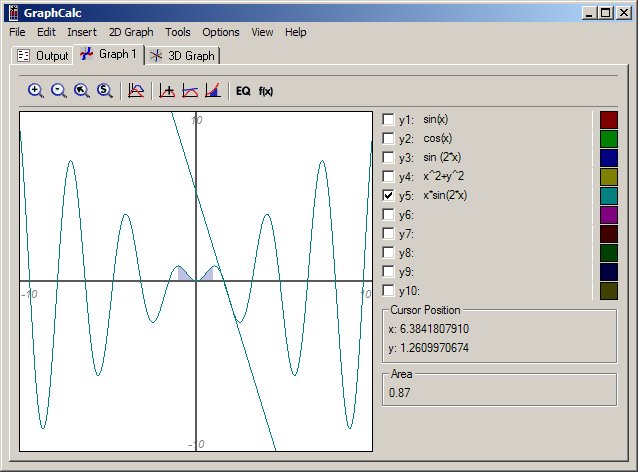
Mostramos cómo podemos realizar operaciones
matemáticas "básicas" para un primer o primeros cursos de
universidad. Analizamos diferentes campos como
Se nos ha ido quedando pequeño el documento.
Ahora incluimos programas para realizar tareas más específicas
y que quizá los otros programas no lo hacen. De momentos hemos añadido
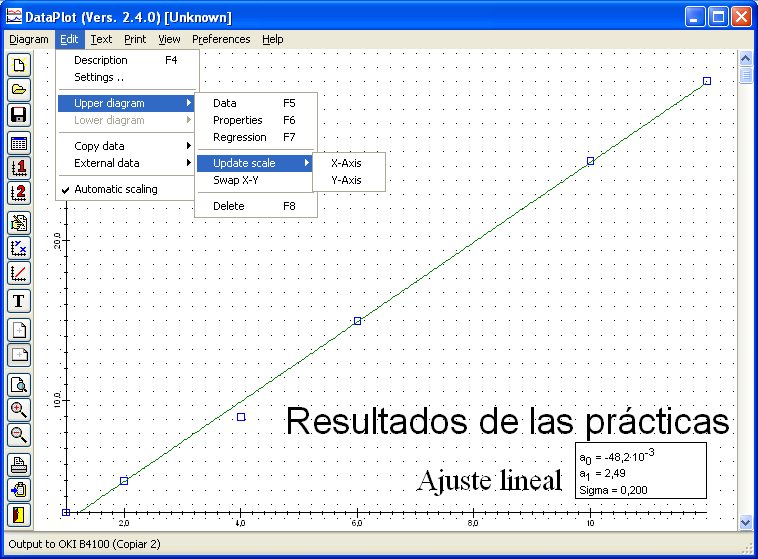
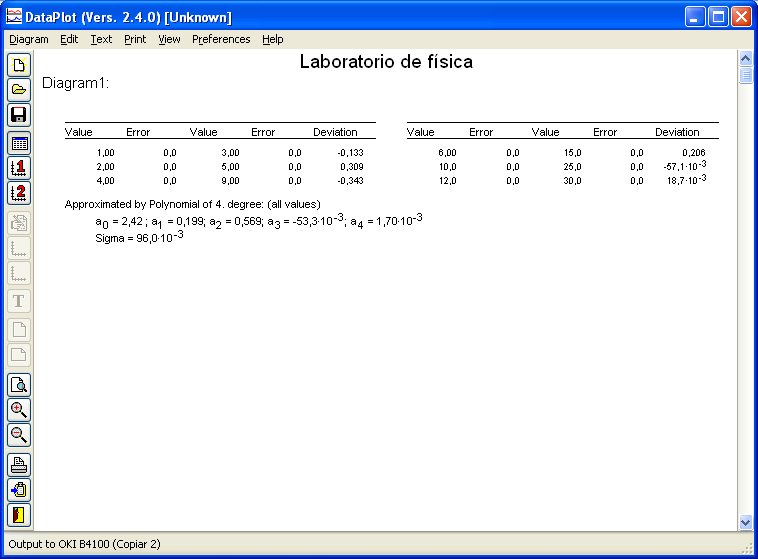
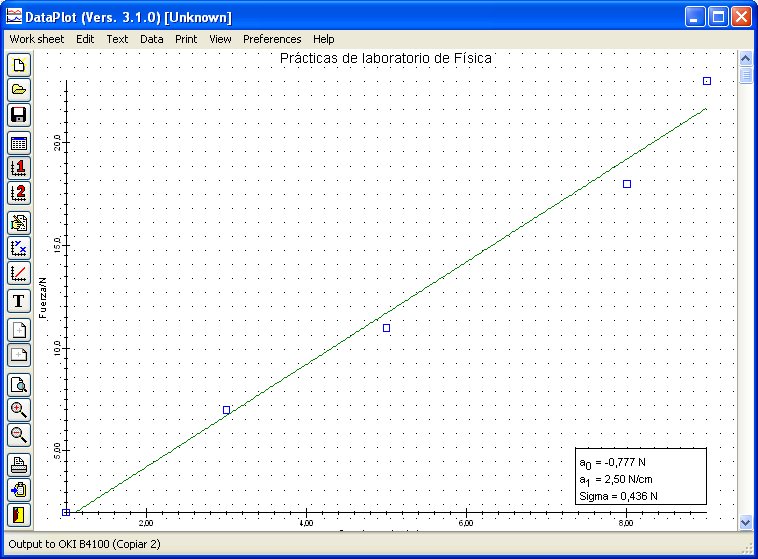
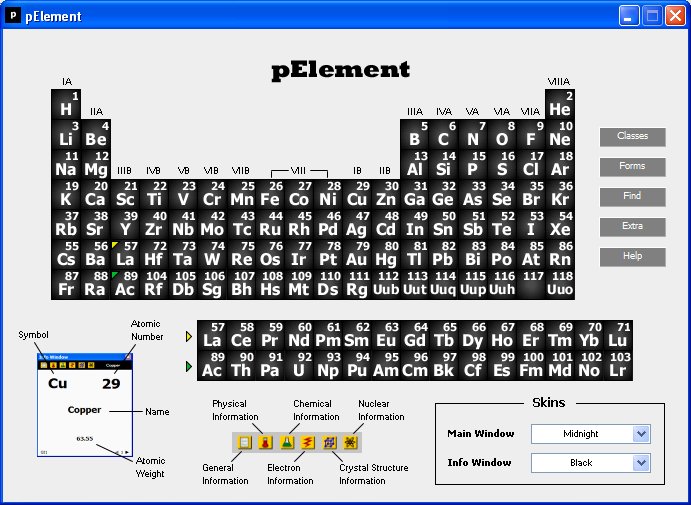
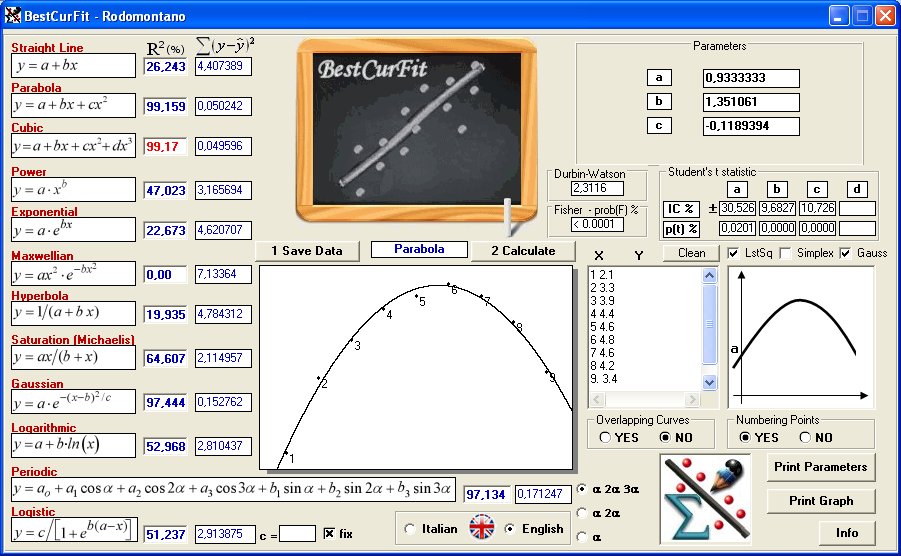
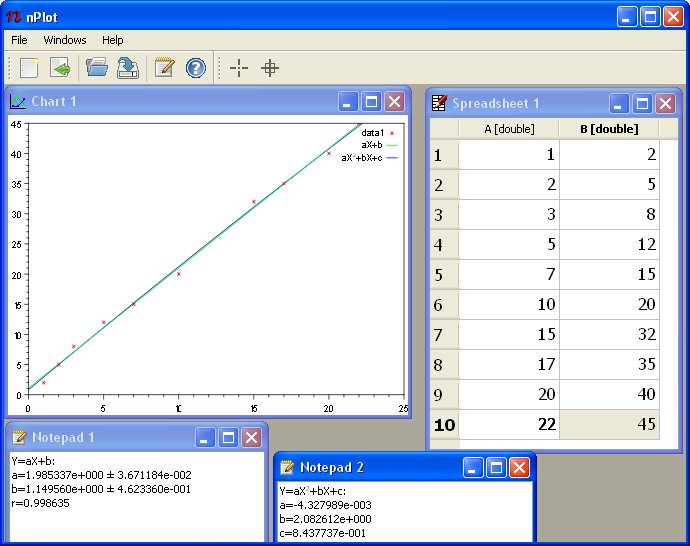
un programa para dibujar datos y realizar regresiones Dataplot
y una tabla periodica de los elementos pElement.
Sencillo. En principio iba a ser sólo una
pequeña introducción a Yacas pero podo a poco hemos ido ampliando
la información a otros programas.
| Yacas |
Ejemplo |
Comentarios
¿Qué estamos calculando? |
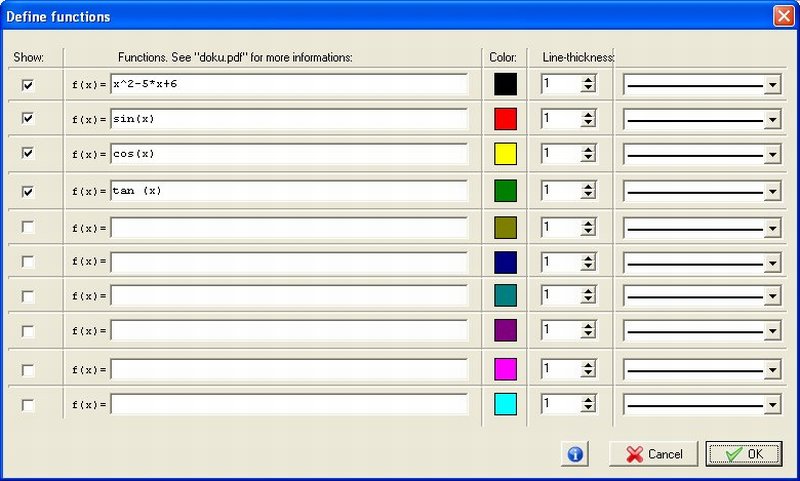
| Funciones
elementales |
Sin(x),Cos(x), Tan(x), Cot(x), Sec(x), Csc(x)
ArcSin(x), ArcCos(x), ArcTan(x) |
Funciones trigonométricas
Funciones trigonométricas inversas |
|
Sinh(x),Cosh(x),Tanh(x),Coth(x),Sech(x)
ArcSinh(x), ArcCosh(x), ArcTanh(x) |
Funciones hiperbólicas
Funciones hiperbólicas inversas |
|
Exp(x), Ln(x), Sqrt(x), Erf(x), Sign(x) |
Función exponencial, logaritmo (neperiano), raíz cuadrada,
error, signo de un número |
| Constantes matemáticas |
Pi, Infinity |
p e infinito |
| Funciones especiales |
|
|
|
Función Gamma de Euler
|
Gamma(1.3)
N(Gamma(1.3),5) |
Calculamos la función Gamma de Euler de 1.3 con 5 decimales |
|
Función Zeta de Riemann
|
N(Zeta(1.3),5) |
|
|
Números de Bernoulli
|
Bernoulli(4) |
|
|
Polinomios de Bernoulli
|
Bernoulli(4,x) |
|
|
Polinomios de Legendre
|
OrthoP(3, x) |
Polinomio de Legendre de tercer orden: P3 (x) = (5 x3
- 3x) / 2 |
|
Polinomios de Chebyshev
|
OrthoT(3, x) |
|
| Operaciones
elementales |
|
|
|
Suma de números o fracciones
|
1+3
1/2+1/3
N(%) ó N(1/2+1/3)
N(1/2+1/3,3) |
.
Da el resultado en forma de fracción: 5/6
Resultado numérico: ajustaría el resultado a los decimales
por defecto
Ajusta el resultado a tres decimales (pero ATENCIÓN, NO REDONDEA,
sino que se queda con los tres primeros decimales) |
|
N(2/3,3) |
Da el resultado de la fracción 2/3 con tres decimales sin redondear.
Esto esto: da como resultado 0,666 (en vez de 0,667 que sería el
resultado con tres decimales) |
|
Raiz cuadrada
|
Sqrt(8) |
Si queremos el valor numérico, N(Sqrt(8)) |
|
Descomponer un número en factores
|
Factor(50) |
Descomponemos el número 50 en producto de factores |
|
Valor numérico con cierto número de decimales
|
N(Sin(2),4)
N(Sqrt(2),5) |
Seno de 2 radianes, con cuatro decimales
Raíz cuadrada de 2 con cinco decimales. |
|
Cociente de una división de dos números
|
Div(10,3) |
Determina el cociente (entero de dos números). En este caso
obtendríamos 3 |
|
Resto de una división de dos números
|
Mod(10,3) |
Determina el resto de una división de dos números. En
este caso obtendríamos 1 |
|
Máximo comun divisor
|
Gcd (2,5) |
Máximo común divisor del 2 y el 5 |
|
Mínimo común múltiplo
|
Lcm (2,5) |
Mínimo común múltiplo del 2 y el 5 |
|
Precisión de los cálculos
|
GetPrecision()
Precision(4) |
Señala el número de decimales con que trabaja. Por defecto,
son 10.
Mostraría 4 decimales en los resultados |
|
Simplificar una expresión
|
Simplify((x+1)*(x-1))
Simplify((x+y)^2-(x-y)^2) |
|
|
Desarrollar una expresión
|
Expand(1-x)^3)
Expand((1+x-y)^2,x) |
Desarrolla el cubo: (1 - x)3
Desarrolla (en x) la expresión (1 + x - y)2 |
|
Dar un valor a una variable
|
a:= 3
Set (a,3) |
Damos a "a" el valor 3. Con dos puntos : e igual = |
|
Borrar el contenido de una variable
|
Clear (a)
Clear (a,b) |
Borramos el contenido de la variable "a"
Borramos el contenido de las variables "a" y "b" |
|
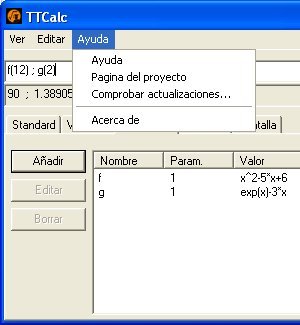
Definir una función
y evaluarla en un punto
|
f(x):=x^2-5*x+1
f(5) |
Definimos la función f(x) = x2 - 5x + 1
... y la evaluamos en el punto x=5 |
|
f(x,y):=3*x-2*y^2
f(2,3) |
Definimos la función de dos variables f (x,y) = 3 x - 2 y2
... y la evaluamos en el punto (2,3) |
| Combinatoria |
|
|
|
Factorial de un número
|
4! |
Calculamos el factorial de 4. 4 ! = 4·3·2·1 |
|
Doble factorial
|
4!! |
4 !! = 4·2 (vamos de 2 en 2, en vez de 1 en 1) |
|
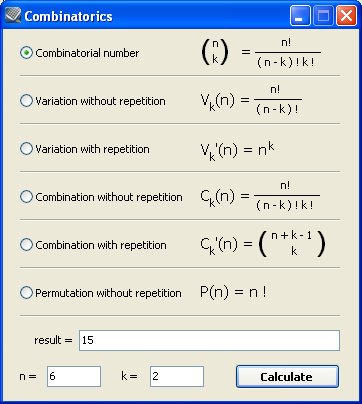
Combinaciones
|
Bin(6,2) |
Calcula el número combinatorio 6 sobre 2, esto es: (6·5)
/ 2! |
|
Permutaciones
|
Permutations({1,2,3}) |
|
| Resolución
de ecuaciones |
|
|
|
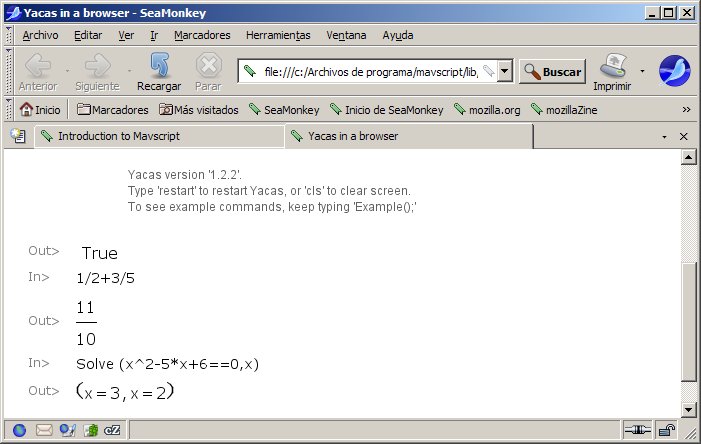
Solve(3*x-5==x+1,x) |
Resolviendo la ecuación: 3 x - 5 = x + 1 |
|
Solve(x/(1+x) == a, x) |
|
|
Solve(x^2-5*x+6 == 0, x) |
Resolución de una ecuación de segundo grado. |
|
Número de raíces reales de un polinomio
|
NumRealRoots(x^2-5*x+6) |
Nos da el número de raíces reales de la ecuación
polinómica x2-5x+6=0 |
|
Resolución de sistemas
|
Solve({x+y==2,x-y==0},{x,y}) |
Resolviendo el sistema:
x + y = 2
x - y = 0 |
|
Solve({x+y+z==1,x-y-z==2,x-y+z==3},{x,y,z}) |
Resolviendo el sistema:
x + y + z = 1
x - y - z = 2
x - y + z = 3 |
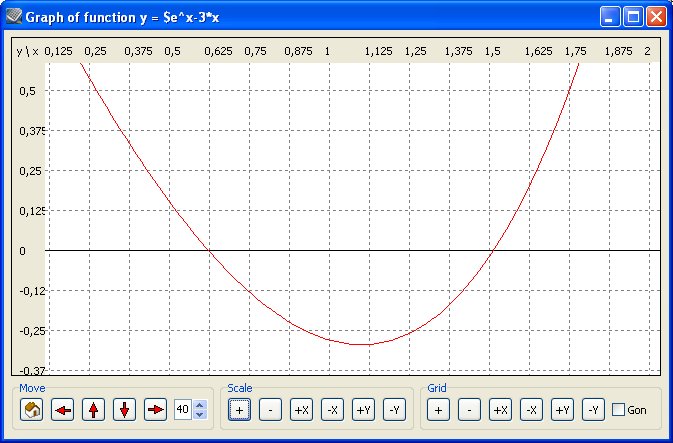
| Método de Newton |
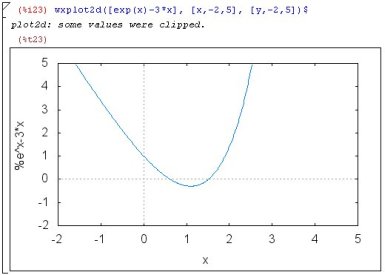
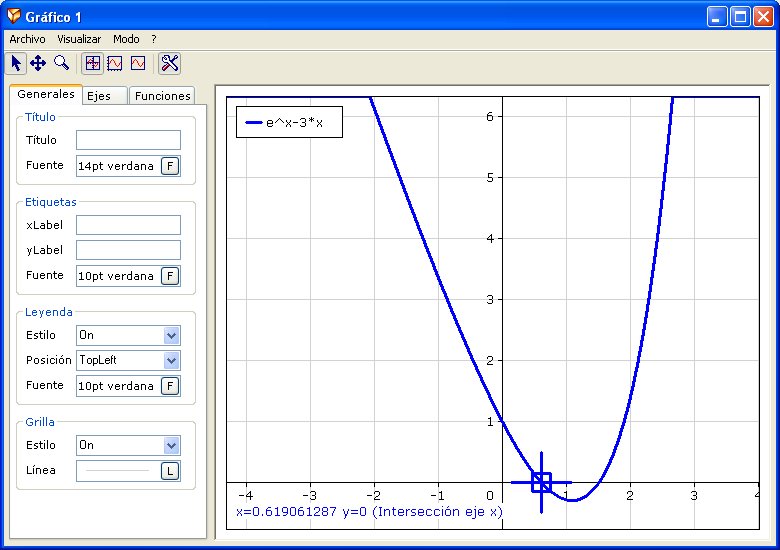
Newton(Exp(x)-3*x,x,1,0.01) |
Resolviendo la ecuación ex - 3 x = 0, por el método
de Newton, partiendo del punto inicial xo = 1, con una precisión
de 0,01 |
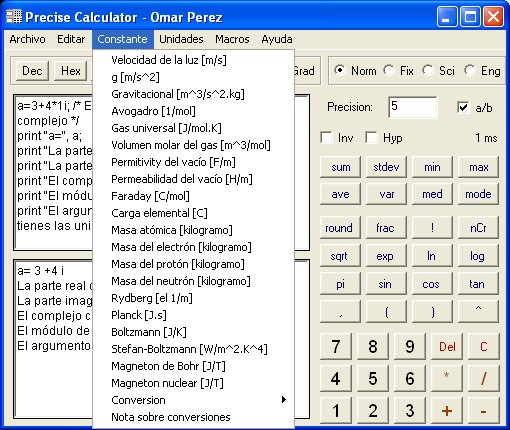
| Operaciones
con números complejos |
Unidad imaginaria: I (mayúscula) |
|
|
1+2*I
ó Complex(1,2) |
Un número complejo |
|
Abs (2+3*I) |
Módulo del número complejo 2 + 3i |
|
Arg (2+3*I)
N(Arg (2+3*I))
N(Arg (2+3*I),3) |
Argumento (en radianes) del número complejo 2 + 3i
... con los decimales por defecto
... con tres decimales |
|
Re(2+3*I) |
Parte real del número complejo 2 + 3 i |
|
Im(2+3*I) |
Parte imaginaria del número complejo 2 + 3 i |
|
Conjugate(2+3*I) |
Coomplejo conjugado del número 2 + 3 i |
|
(3+4*I)+(1-3*I)
ó Complex(3,4)+Complex(1,-3) |
Suma de dos números complejos |
|
(3+4*I)*(1-3*I) |
Producto de dos números complejos |
|
(3+4*I)/(1-3*I) |
Cociente de dos números complejos |
| |
(1+2*I)^2 |
(1 + 2 i)2 |
|
Ln(3+4*I) |
Logaritmo neperiano de un número complejo |
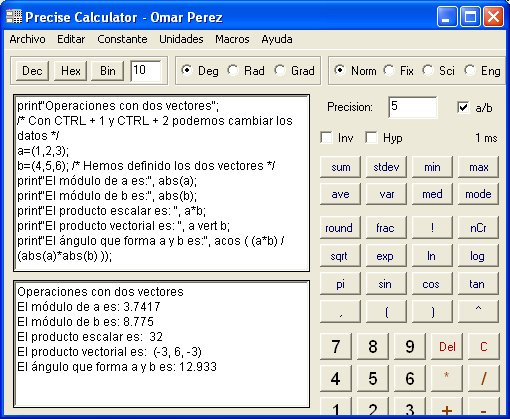
| Operaciones
con vectores |
|
|
|
Módulo de un vector
|
Norm({3,4})
o bien: a:={3,4}
Norm(a) |
Módulo de un vector (32 + 42)1/2 |
|
Normalizar un vector
|
Normalize ({3,4}) |
Normalizar un vector. Esto es, dividir el vecto rentre su módulo |
|
Suma de vectores
|
{1,2,3}+{4,5,6}
o bien: a:={1,2,3};
b:={4,5,6};
a+b |
|
|
Multiplicación por un escalar
|
3*{1,2,3}
o bien: a:={1,2,3}
3*a |
|
|
Producto escalar
|
Dot({1,2},{4,5})
InProduct({1,2},{4,5})
o bien: a:={1,2}
b:={4,5}
Dot(a,b)
o bien: InProduct(a,b)
o bien: a.b |
Producto escalar de los vectores (1,2) y (4,5)
(1,2)·(4,5)=1·4+2·5=14
Para calcular el producto escalar de dos vectores podemos emplear el
punto . ó Dot ó InProduct |
|
Producto vectorial
|
CrossProduct({1,2,3},{4,2,5})
ó a:={1,2,3}
b:={4,2,5}
a X b |
Para calcular el producto vectorial de dos vectores podemos emplearx
o CrossProduct |
|
Base ortogonal
|
OrthogonalBasis({{1,1,0},{2,0,1},{2,2,1}}) |
|
|
Base ortonormada
|
OrthonormalBasis({{1,0,1,0},{1,1,1,0},{0,1,0,1}}) |
Además divide los vectores entre su módulo |
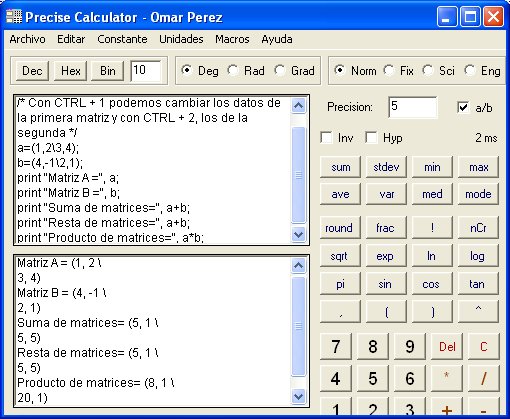
| Operaciones
con matrices |
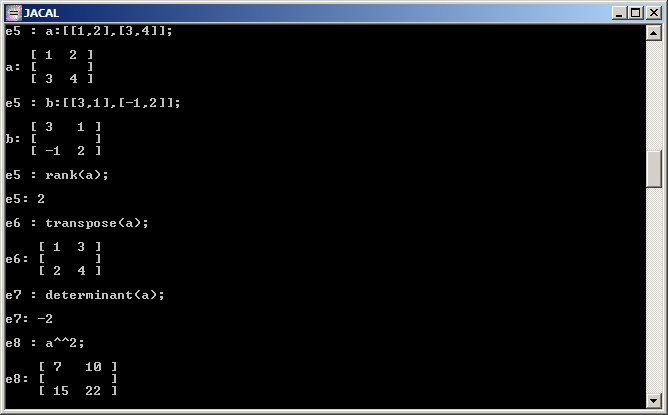
a:={{1,2},{3,4}}
b:={{2,-1},{1,3}} |
Vamos a definir las matrices a y b |
|
Determinante de una matriz (cuadrada)
|
Determinant(a)
Determinant({{1,2},{3,4}}) |
|
|
Traza de una matriz
|
Trace({{1,2},{3,4}})
o bien: a:={{1,2},{3,4}}
Trace(a) |
La traza es la suma de los elementos de la diagonal principal |
|
Matriz traspuesta
|
Transpose (a) |
|
|
Matriz inversa
|
Inverse (a) |
|
|
Producto de matrices
|
a.b
o bien Dot(a,b)
Dot({{1,2,3},{4,5,6}},{{1,2},{3,4},{5,6}})
PrettyForm(%) |
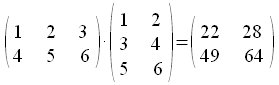 |
|
Menor complementario
|
A:={{1,2,3},{4,5,6},{7,8,9}}
Minor(A,2,3) |
Menor complementario del elemento a2,3 de la matriz A |
|
Polinomio característico
|
a:={{4,2},{-1,1}}
CharacteristicEquation(a,x)
Expand(%,x) |
|
|
Valores propios
|
a:={{4,2},{-1,1}}
EigenValues(a) |
|
|
Vectores propios
|
a:={{4,2},{-1,1}
vp:=EigenValues(a)
EigenVectors(a,vp) |
|
|
Potencia de matrices
|
a:={{4,2},{-1,1}}
MatrixPower(a,2)
sería equivalente a : a.a ; a*a ; a^2 |
Calcula la potencia n-ésima de una matriz cuadrada. En este
caso el cuadrado de la matriz a |
|
¿Es una matriz simétrica?
|
A:={{4,2},{-1,1}}
IsSymmetric(A) |
Devuelve true si la matriz es simétrica (la matriz coincide
con su traspuesta) o false si no lo es. |
|
¿Es una matriz anti-simétrica?
|
A:={{4,2},{-1,1}}
IsSkewSymmetric(A) |
Devuelve true si la matriz es anti-simétrica (la matriz
coincide con su traspuesta cambiada de signo) o false si no lo es. |
|
¿Es una matriz ortogonal?
|
A:={{4,2},{-1,1}}
IsOrthogonal(A) |
Devuelve true si la matriz es ortogonal (cuando la matriz inversa
coincide con la traspuesta) o false si no lo es. |
|
¿Es una matriz idempotente?
|
A:={{4,2},{-1,1}}
IsIdempotent(A) |
Devuelve true si la matriz es idempotente (A2 = A)
o false si no lo es. |
| Resolución
de sistemas |
A:={{1,1,1},{2,-1,3},{3,2,-1}}
b:={6,9,4}
MatrixSolve(A,b)
SolveMatrix(A,b) |
Resolvemos el sistema:
x + y + z = 6
2x -y + 3z = 9
3x + 2y - z = 4 |
|
Factorizacion LU
Método de Doolittle
|
A:={{1,1,1},{2,-1,3},{3,2,-1}}
LU(A) |
Factorización LU de la matriz A por el método de Doolittle
(la matriz L posee 1´s en la diagonal principal) |
|
Factorizacion LU
Método de Cholesky
|
A:={{1,1,1},{2,-1,3},{3,2,-1}}
Cholesky(A)
>Out: no la calcula pues la matriz A no es definida positiva |
A debe ser simétrica y definida positiva |
| Límites |
Limit(x,Infinity) (x^2-1)/(x^2+1) |
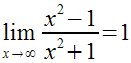 |
|
Límite por la izquierda
|
Limit (x,0,Left) 1/x |
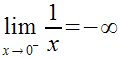 |
|
Límite por la derecha
|
Limit (x,0,Right) 1/x |
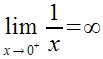 |
| Derivadas |
|
|
|
Primera derivada
|
Deriv(x) 1/(1+x^2)
ó
D(x) 1/(1+x^2) |
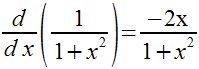 |
|
Segunda derivada
|
D(x,2) x^2+3*x-1
ó bien: D(x) D(x) x^2+3*x-1 |
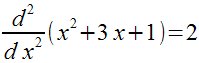 |
|
Derivadas parciales
|
z:=x^2+y^3
D(x) z
D(y) z
o bien
D(x) x^2+y^3 |
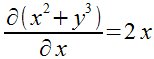
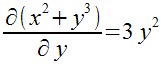 |
|
Matriz jacobiana
|
JacobianMatrix({x^2+y^2,x^3+y^4},{x,y})
JacobianMatrix({x^2+y^2,x^3+y^4,3*z^2},{x,y,z}) |
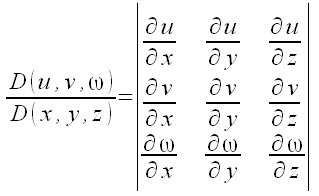 |
|
Matriz wronsquiana
|
WronskianMatrix({Sin(x),Cos(x)}, x)
WronskianMatrix({1,x,x^2}, x) |
|
|
Wronsquiano
|
Determinant (WronskianMatrix({1,x,x^2},x)) |
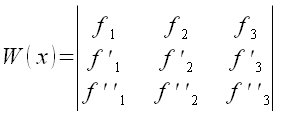 |
|
Matriz hessiana
|
HessianMatrix(x^2+y^2, {x,y}) |
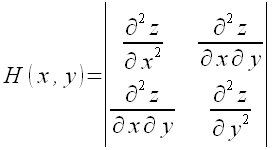 |
|
Gradiente de un escalar
|
D({x,y,z}) Sin(x*y*z) |
Calculamos el gradiente de una función escalar, en este caso
de Sin(x y z)
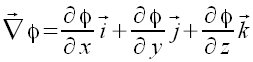 |
|
Divergencia de un vector
|
Diverge({x*y,y*z,x*z},{x,y,z}) |
Calculamos la divergencia de un vector, en este caso del (x y,y z,x
z).
¡¡ Sin embargo NO CALCULA LA SUMA, lo deja indicado !!
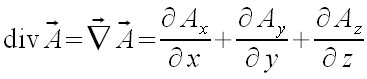 |
|
Rotacional de un vector
|
Curl({x*y,y*z,x*z},{x,y,z}) |
Calculamos el rotacional de un vector, en este caso del (x y,y z,x
z)
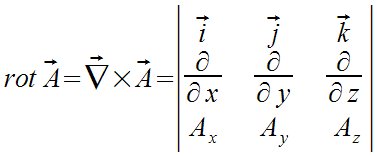 |
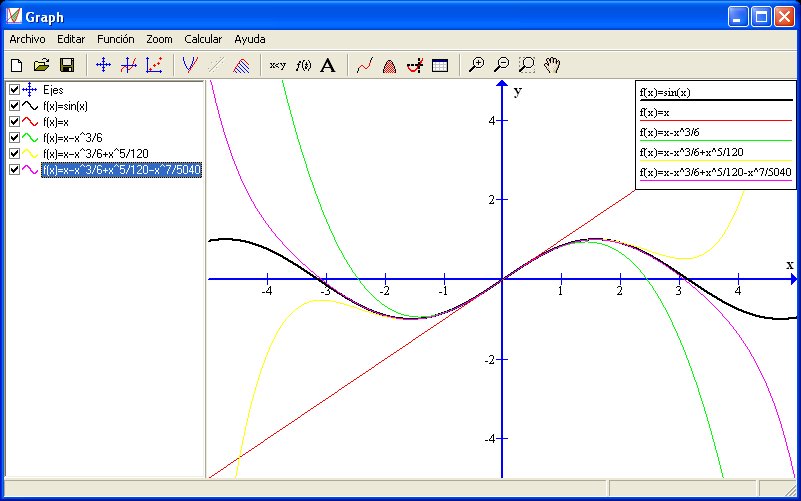
| Desarrollo en serie de Taylor |
Taylor(x,0,5) Sin(x) |
Desarrollo en serie de Taylor de grado 5 (hasta la quinta derivada)
de la función sin (x) en el origen
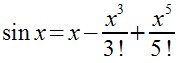 |
|
Taylor(x,0,5) Exp(-x)
PrettyForm(%) |
Desarrollo en serie de Taylor en torno al origen de e-x
Presenta el resultado de forma "bonita" |
|
Taylor(x,1,4) x^4-3*x^3+2*x^2+x+1 |
Desarrollo en serie del polinomio en torno al punto x = 1
O lo que es lo mismo: reescribir el polinomio
en potencias de (x-1) |
| Integrales |
Integrate(x) Sin(x) |
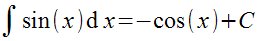 |
|
Integral definida
|
Integrate(x,0,1) x^2 |
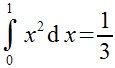 |
|
Integrate(x,a,b) Cos(x) |
|
| Ecuaciones
diferenciales |
|
|
|
Resolución de ecuaciones
|
OdeSolve(y'+y==0) |
Resolvemos la ecuación diferencial y' + y = 0 |
|
OdeSolve(y'==2*y) |
Resolvemos la ecuación diferencial y' = 2 y |
|
OdeSolve(y''+y==0) |
Resolvemos la ecuación diferencial y'' + y = 0 |
|
Comprobación de soluciones
|
OdeTest(y''-5*y'+6*y,Exp(2*x)+Exp(3*x)) |
Comprueba que e2x+e3x es solución de la
ecuación diferencial y''-5y'+6y=0 |
|
Orden de una ecuación diferencial
|
OdeOrder(y''-5*y'+6*y==0) |
|
| Transformada
de Laplace |
LaplaceTransform(t,s,t^2) |
Transformada de Laplace (en función de s) de la función
t2
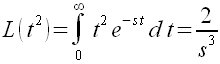 |
|
|
|
| Sumatorios
y "productorios" |
|
|
|
Sumatorio
|
Sum(k,1,n,k^2) |
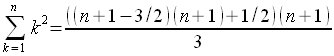 |
|
Productorio
|
Factorize(k,1,n,k^2) |
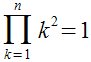 |
| Polinomio
interpolador |
Polinomio interpolador de Lagrange que se ajusta a unos puntos |
|
|
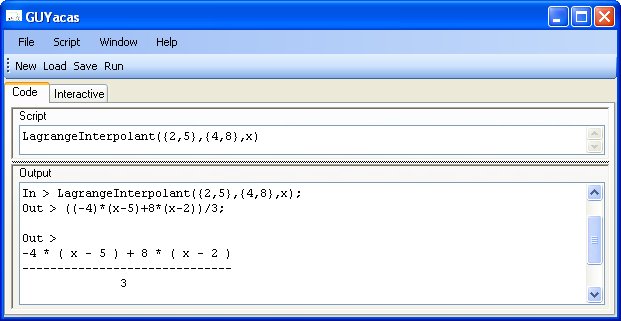
f(x):=LagrangeInterpolant({2,5},{4,8},x)
f(3)
Simplify(f(x))
LagrangeInterpolant({2,5},{4,8},x) |
Los valores en la primera llave {} son los de la "x"
los de la segunda llave {} los de la "y"
Polinomio interpolador que pasa por los puntos (2,4) y (5,8) |
|
f(x):=LagrangeInterpolant({0,1,3},{-2,6,40},x)
Simplify(f(x)) |
Polinomio interpolador que pasa por los puntos (0,-2), (1,6) y (3,40) |
| Importación/
Exportación |
|
|
|
Guardar un resultado en un fichero
|
ToFile("datos.txt") [PrettyForm(D(x) x/(1+x^2));] |
Exporta al fichero datos.txt el resultado de la derivada de la función
x/(1+x2) |
|
exportando a LaTeX
|
TeXForm(D(x) x/(1+x^2)) |
Exporta al formato Latex el resultado de la derivada de la función
x/(1+x2) |
| Mathomatic |
Ejemplo |
Comentarios
¿Qué estamos calculando? |
| Salida de la aplicación |
quit |
|
| Obtención de ayuda |
help
help derivative
help all >manual.txt |
ayuda en general
ayuda de un comando concreto, en este caso derivative
podemos exportar las ayuda de todos los comandos al archivo manual.txt |
| Precisión en los cálculos |
set precision 4 |
Ajusta a 4 el número de decimales |
|
e, pi, i
e^(i*pi) |
-1 |
| Operadores |
+ - * / !
^ ó **
10 // 3
10 % 3 |
suma, resta, producto, cociente, factorial
potencia
cociente (entero). En este caso da como resultado: 3
resto de la división. En este caso dará: 1 |
| Definir una función y evaluarla en varios puntos |
3x-2y=5
solve y
calculate |
A partir de la ecuación de partida
despejamos la "y"
nos pedirá el valor de "x" para calcular la correspondiente
"y" |
|
x+2y+3z-10=0
solve z
calculate |
A partir de la ecuación de partida
despejamos la "z"
nos pedirá los valores de "x" e "y" para calcular la correspondiente
"z" |
| División de polinomios |
divide |
Después de introducir el dividendo y el divisor, calcula el
cociente y el resto |
|
divide x x^2-1 2x+1 |
Directamente calcula el cociente y el resto de la división (x2-1)
/ (2x+1) |
| Operaciones con fracciones |
2/x-5/y
fraction
unfactor fraction |
- Suma las fracciones anteriores sacando común denominador
- Vuelve a dejar las fracciones como estaban |
|
x*(3-y)
unfactor |
Quita los factores comunes |
| Resolución de ecuaciones |
x+5=3x+1
solve |
Se nos pedirá la variable a resolver: x
O directamente solve x |
|
3x+2y-5=0
solve y |
Despeja la "y" |
|
2^x=3
solve x |
|
|
2*(x-1)+3*x=5*(1-x)+3*(2+x)
simplify
solve verify x |
Podemos escribir una ecuación
... simplificarla
... resolverla verificando la solución |
| Sistemas de ecuaciones |
x+y=5
x-y=1
eliminate y
solve x |
Tras escribir el sistema, despejamos la "y" de ambas ecuaciones y las
igualamos. A continuación resolvermos x |
| Operaciones con números complejos |
|
|
|
(3+2i) + (1-i)
(3+2i)(1-i)
(3+2i)/(1-i) |
Suma, producto y cociente de números complejos |
|
real |
Señala la parte real del número complejo |
|
imaginary |
Señala la parte imaginaria del número complejo |
|
Raíz n-ésima de un número complejo
|
roots |
Pide el índice, la parte real y la parte imaginaria y obtiene
las raíces |
|
roots 2 3 4 |
Calcula la raíz cuadrada del número complejos 3 + 4 i |
|
(3+2i)(1-i) |
|
| Límites |
2x/(x+1)
limit |
Se nos pedirá a qué valor tiende el límite. Para
infinito ponemos inf
O directamente limit x inf |
| Derivadas |
|
|
|
x^3+x^2+x+1
derivative
ó differentiate |
Escribimos la función en primer lugar y a continuación
el comando derivative |
|
Derivada de segundo orden
|
x^3+x^2+x+1
differentiate x 2 |
Calcula la segunda derivada de la función respecto de la variable
x |
|
Derivadas parciales
|
x^2+y^3
derivative x
derivative y |
Calculamos las derivadas parciales, respecto de x e y, de la función
anterior |
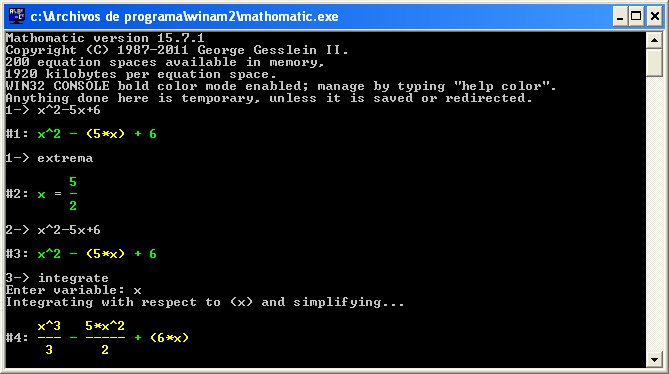
| Cálculo de máximos y mínimos de una función |
x^2-5*x+6
extrema |
Calcula los máximos y los mínimos de una función
(no especifica si se trata de un máximo o de un mínimo) |
| Integrales |
Sólo integra polinomios |
|
|
Integral indefinida
|
x^3+x^2+x+1
integrate
ó integral |
Escribimos la función en primer lugar y a continuación
el comando integrate. Se nos pedirá la variable de integración
(x)
O podemos escribirla directamente integrate x |
|
Integral definida
|
x^3+x^2+x+1
integral definite |
|
|
Integración numérica
|
x^0.5/(1-x^3)
nintegrate x |
Después de que se nos avisa de que hay una singularidad, se
introduce los límites de integración inferior y superior.
Utiliza la regla de Simpson |
|
Integración numérica
|
nintegrate trapezoid x |
Después de que se nos avisa de que hay una singularidad, se
introduce los límites de integración inferior y superior.
Utiliza la regla del trapecio |
| Desarrollo en serie de Taylor |
e^x
taylor |
Se nos pedirá el torno a qué punto queremos obtener el
desarrollo en serie de Taylor así como el número de derivadas
a tomar (el orden) |
|
e^x
taylor x 5 0 |
Calcula el desarrollo en serie de Taylor en torno al origen de la función
e^x hasta grado 5 |
| Transformada de Laplace |
y=1
laplace
y=x^2
laplace |
- Se nos pedirá la variable (x). O podemos escribir directamente
laplace
x. El resultado es la transformada de Laplace de 1 que es 1/x
- La transformada de Laplace de x2 es 2/x3 |
| Transformada inversa de Laplace |
y = 1/x
laplace inverse x |
- Dará como resultado 1. |
| Sumatorio |
y=x^2
sum |
Se nos pedirá desde dónde empieza la suma y hasta dónde
acaba. |
| "Productorio" |
y=x^2
product |
Se nos pedirá desde dónde empieza el producto y hasta
dónde acaba. |
| Comparar expresiones |
compare with
número de ecuación |
|
| Pari/GP |
Ejemplo |
Comentarios
¿Qué estamos calculando? |
| Ayuda |
? |
|
| Comentarios |
\\ |
Podemos añadir comentarios con \\ tras la operacion |
| Visualizar resultados anteriores |
%15 |
Visualizar el resultado 15 |
| Salir de la aplicación |
quit |
|
| Constantes |
Pi , I, Euler |
Constante de Euler = 0,57721... |
| Funciones |
|
|
|
Funciones trigonométricas
|
sin(x), cos(x), tan(x), cotan(x) |
|
|
Funciones trigonométricas inversas
|
asin(x), acos(x), atan(x) |
|
|
Funciones hiperbólicas
|
sinh(x), cosh(x), tanh(x) |
|
|
Funciones hiperbólicas inversas
|
asinh(x), acosh(x), atanh(x) |
|
|
Raíz cuadrada
|
sqrt(x) |
Raíz cuadrada de x |
|
Raíz n-ésima
|
sqrtn(x,n)
ej. sqrtn(27,3) |
|
|
Funciones exponenciales y logarítmicas
|
exp(x)
log (x) |
log (x) es el logaritmo neperiano (en base e) |
|
Otras funciones
|
gamma(x) |
Función Gamma de Euler.
También trabaja con funciones de Bessel, Zeta de Riemann... |
| Operaciones elementales |
|
|
|
Operaciones básicas
|
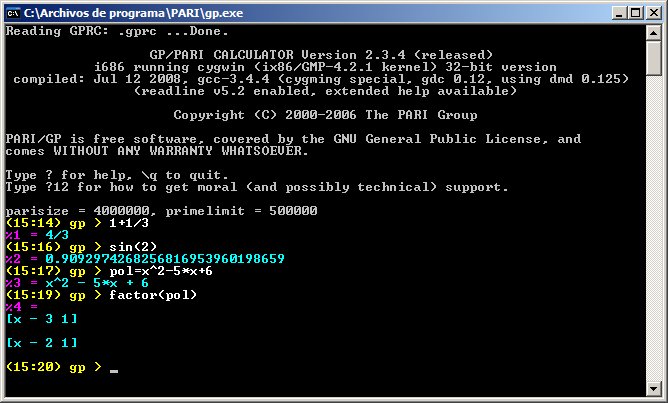
+ - * / ^
1+1/3 |
Da el resultado en forma de fracción |
|
Factorial de un número
|
factorial(4)
4! |
|
|
Operaciones con números
|
|
|
|
Números aleatorios
|
random(N)
ej. random(11) |
número aleatorio entre 0 y N-1
número aleatorio entre 0 y 10 |
|
Divisores de un número
|
divisors (125) |
Da los divisores de 125 |
|
Máximo común divisor
|
gcd(2,10) |
Máximo común divisor de los números 2 y 10 |
|
Mínimo común múltiplo
|
lcm(2,10) |
Mínimo común múltiplo de los números 2
y 10 |
|
x=[12,6,18,24]
lcm(x) |
Definimos la lista de números 12, 6, 18 y 24.
Calculamos su mínimos común múltiplo |
|
¿Es un número primo?
|
isprime(45) |
Responde 1 si es cierto y 0 si es falso |
| Desarrollando y simplificando expresiones |
|
|
|
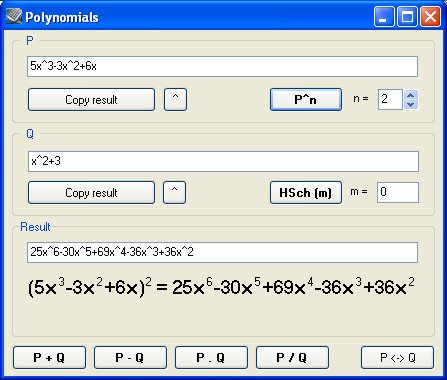
Desarrollo de expresiones
|
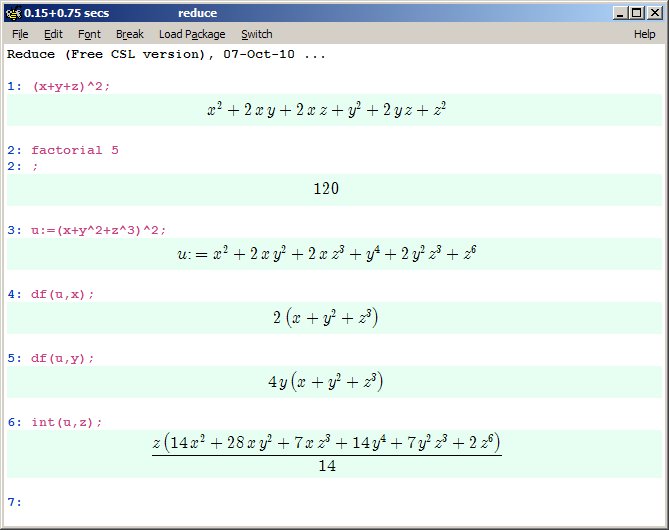
(x+y+z)^2 |
|
|
Simplificando expresiones
|
simplify (x+3*x-5*x+4-2*x+1) |
|
|
Operaciones con polinomios
|
|
|
|
Definiendo un polinomio
|
pol=x^2-5*x+6 |
|
|
Descomponiendo un polinomio en producto de factores
|
factor (pol) |
|
|
Grado de un polinomio
|
poldegree(pol) |
|
|
Derivando el polinomio
|
deriv(pol,x) |
|
|
Integrando el polinomio
|
intformal(pol,x) |
|
|
Polinomios especiales
|
pollegendre(n)
poltchebi(n) |
Polinomio de Legendre de grado n
Polinomio de Chevichef de grado n |
| Definiendo y represantando funciones |
f(x)=x^2-5*x+6 |
Definimos la función f (x) = x2 - 5 x + 6 |
|
Evaluando en un punto
|
f(1) |
Evaluamos la función anterior en el punto 1 |
|
Representando la función
|
ploth(x=-5,5,f(x)) |
Representa la función f (x) definida anteriormente desde x =
-5 a x = 5 |
|
plot(x=-2,2,sin(x)) |
Dibuja la función sin (x) en la consola, en plan cutrillo... |
|
ploth(x=-2,2,sin(x)) |
Lo dibuja bien, en una ventana aparte. |
| Operaciones con números complejos |
x+I*y |
|
|
a=3+4*I
b=1-2*I
a+b , a-b , a*b , a/b, a^2 |
Definimos los números complejos a y b |
|
Módulo de un número complejo
|
abs(a) |
|
|
Argumento de un número complejo
|
arg(a) |
|
|
Complejo conjugado
|
conj(3+4*I) |
|
|
Parte real de un número complejo
|
real(a) |
|
|
Parte imaginaria de un número complejo
|
imag(a) |
|
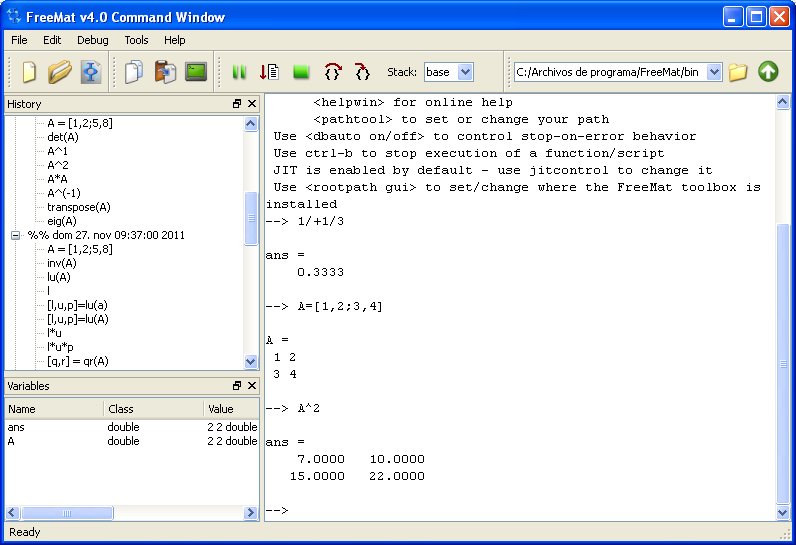
| Operaciones con matrices |
a=[1,2;3,4] |
Definiendo una matriz |
|
Dimensiones de la matriz a
|
matsize(a) |
|
|
Rango de una matriz
|
matrank(a) |
|
|
Determinante de la matriz a
|
matdet(a) |
|
|
Traspuesta de un matriz a
|
mattranspose(a) |
|
|
Núcleo de la matriz a
|
matker(a) |
|
|
Polinomio característico de la matriz a
|
charpoly (a) |
|
|
Polinomio mínimo de a
|
minpoly(a) |
|
|
Vectores propios de a
|
mateigen(a) |
|
|
Valores y vectores propios de la matriz real simétrica
a
|
qfjacobi(a) |
|
| Resolución de sistemas de ecuaciones |
a=[1,2;3,4]
b=[5;6] |
Atención a cómo hemos escrito la matriz de los términos
independientes, como un vector columna ; |
|
matsolve(a,b) |
Utiliza el método de eliminación gaussiana |
| Derivación |
(3*x^2-5*x+1)' |
|
|
(3*x+5*y)' |
Deriva con respecto de x |
| Desarrollo en serie de Taylor |
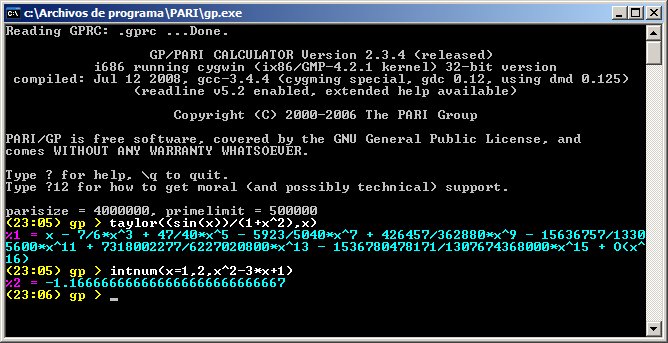
taylor(sin(x),x)
taylor(1/(x^2+1),x) |
Desarrollo en serie de Taylor en torno al origen: |
| Integración numérica |
intnum(x = 0,1, sin(x^2)) |
|
| Sumatorios |
sum(i=1, 10, i^2) |
Suma i2 desde i = 1 hasta i = 10 |
| Interpolación polinómica |
x=[1,2,3]
y=[4,5,6] |
|
|
polinterpolate(x,y) |
Polinomio interpolador que pasa por los puntos (1,4), (2,5), (3,6) |
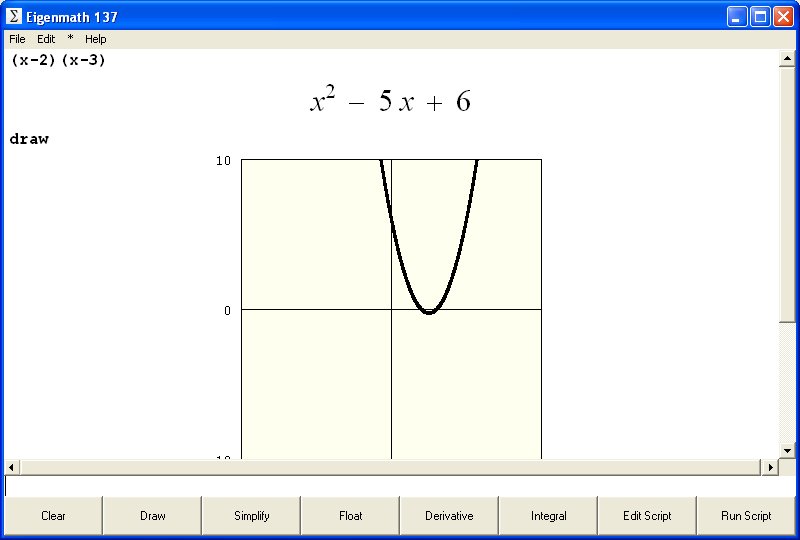
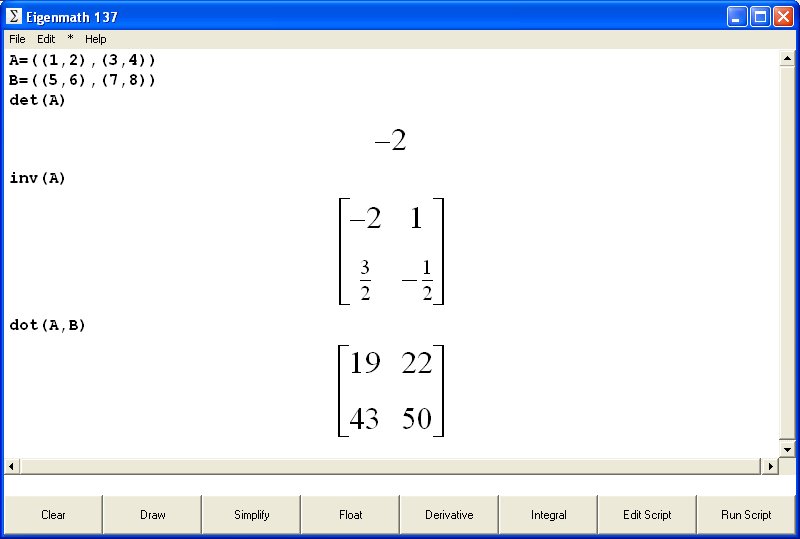
| Eigenmath |
Ejemplo |
Comentarios
¿Qué estamos calculando? |
|
|
El programa distingue entre mayúsculas y minúsculas |
| Operaciones con números complejos |
z1=3+4*i
z2=-2+3*i |
Definimos los números complejos z1 y z2 |
|
z1+z2
z1-z2
z1*z2
z1/z2 |
|
| Operaciones con vectores |
a=(1,2,3)
b=(4,5,6) |
|
|
Suma de vectores
|
a+b |
O la resta a- b |
|
Producto escalar
|
dot(a,b) |
|
|
Producto vectorial
|
cross(a,b) |
|
| Operaciones con matrices |
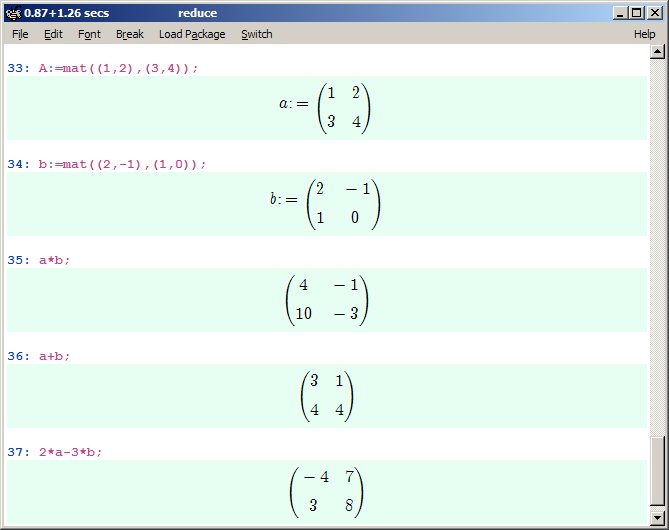
A=((1,2),(3,4))
A=((5,6),(7,8)) |
Definimos las matrices A y B |
|
Determinante de A
|
det(A) |
Atención, no debe dejarse un espacio en medio: no es correcto
escribir det (A) |
|
Inversa de A
|
inv(A) |
|
|
Matriz adjunta de A
|
adj(A) |
Nos da la adjunta de la traspuesta (o la trapuesta de la adjunta) |
|
Suma y resta de matrices
|
A+B ; A - B |
|
|
Producto de matrices
|
dot(A,B) |
|
| Derivadas |
f=x^2-5*x+6 |
|
|
Primera derivada
|
d(f,x)
d(f) |
También podemos emplear la palabra derivative:
derivative(f,x) |
|
Segunda derivada
|
d(f,x,2) |
|
|
Derivadas parciales
|
g=x^2+y^2-2*x*y-3*x+2*y+1 |
|
|
Derivadas parciales primeras
|
d(g,x)
d(g,y) |
Derivada parcial de g respecto de x
Derivada parcial de g respecto de y |
|
Derivadas parciales segundas
|
d(g,x,2) ó d(g,x,x)
d(g,x,y)
d(g,y,2) ó d(g,y,y) |
Respecto de x dos veces
Cruzada, respecto de x y respecto de y (o al revés)
Respecto de y dos veces |
| Función escalar |
F=x^2+y^2-2*x*y-3*x+2*y+1 |
|
| Función vectorial |
G=(x^2-3*x*y,y^3-2x+y,2*z) |
|
| Gradiente de un escalar |
d(F,(x,y)) |
Nos da el gradiente como vector columna |
|
Divergencia de un vector
|
div(U)=d(U[1],x)+d(U[2],y)+d(U[3],z) |
Definimos en primer lugar lo que es la divergencia |
|
div(G) |
Calculamos la divergencia de la función G definida anteriormente |
|
Rotacional de un vector
|
rot(U)=(d(U[3],y)-d(U[2],z),
d(U[1],z)-d(U[3],x),d(U[2],x)-d(U[1],y)) |
Definimos en primer lugar lo que es el rotacional |
|
rot(G) |
Calculamos el rotacional de la función G definida anteriormente |
|
Laplaciana de una función escalar
|
laplaciana(U)=d(U,x,2)+d(U,y,2)+d(U,z,2) |
Tampo está definida, pero podemos hacerlo |
|
laplaciana(F) |
|
| Desarrollo en serie de Taylor |
taylor(sin(x),x,5) |
Recordemos que hay que escrbirlo con minúsculas (taylor). Desarrollo
en serie de Taylor de grado 5 (hasta la quinta derivada) de la función
sin (x) en el origen |
| Integrales |
|
|
|
Integral indefinida
|
integral(x^2-5*x+6,x)
integral(x^2-5*x+6) |
También podemos definir la función: f=x^2-5*x+6
integral(f,x) ó integral(f) |
|
Integral definida
|
defint(x^2,x,-1,1) |
Integral definida de la función x2 entre -1 y 1 |
|
Integral doble
|
integral(x*y,x,y) |
|
|
Integral curvilínea
|
x=t
y=t^2
z=t^3
g=(x,y,z)
F=(x*z^2,x*y,z*y^3)
defint(dot(F,d(g,t)),t,0,1) |
Queremos evaluar la integral de línea ò
x
z2 dx + x y dy + z y3 dz a lo largo del camino x
= t, y = t2, z = t3 desde t = 0 a 1 |
| Sumatorios y "productorios" |
|
|
|
sum(k,1,100,k) |
Suma de los 100 primeros números naturales |
|
sum(k,1,n,k^2)
sum(k,1,10,k^2) |
No permite un "n" genérico
Suma de 1 a 10 de k2 |