|
Página inicial (antes en http://es.geocities.com/fisicas - http://www.carrascal.net46.net/fisicas/ - https://carrascal.000webhostapp.com/fisicas/ - https://castrillodonjuan.000webhostapp.com/fisicas/ https://nuestrospueblos.000webhostapp.com/fisicas/ - https://kddj.000webhostapp.com/fisicas/ ) Dirección actual: https://castrillodedonjuan.com/fisicas/ Desde mi blog se puede acceder a la última dirección disponible: http://matematicasfisicaquimicauva.blogspot.com/ Sugerencia, ideas y comentarios: fisicas@yahoo.es Esta sección fue creada el 15/03/2011. Última actualización: 22/12/2014. Última comprobación de versiones: 06/07/2017. |
[Historial de cambios] [¿Dónde conseguir LibreOffice?] [Algunas ideas para facilitar la escritura de fórmulas con LibreOffice] [Varios ejemplos (33) de fórmulas] [Alfabeto griego] [Herramientas adicionales] [Opiniones recibidas por correo electrónico]
Todos los ejemplos que se indican se han planteado
para LibreOffice Math. En principio serían perfectamente
válidos para Apache OpenOffice, aunque
algunas letras griegas cambian su nombre (por lo que deberá
tenerse en cuenta si se quiere utilizar Apache OpenOffice). Se incluyen
un montón de ejemplos de fórmulas de diferentes campos: matemáticas
(álgebra, cálculo, ecuaciones diferenciales, métodos
numéricos...), física (mecánica, electromagnetismo,
física cuántica, física nuclear...), química...
|
|
|
|
¿Dónde conseguir LibreOffice?En la página oficial en castellano: http://es.libreoffice.org/ en la sección de descargas: http://es.libreoffice.org/descarga/ . En el momento de redactar este texto por primera vez (15/03/2011) se encuentra en la versión (en castellano) 3.2.1 y ocupa unos 213 MB. A fecha 01/08/2017, se encuentra en la versión 5.4.1.0. Ocupa 213 MB. No os olvidéis descargar también el archivo de ayuda en castellano (que ocupa unos 10 MB).
¿Dónde conseguir Apache OpenOffice? En la página oficial en castellano: http://www.openoffice.org/ . A fecha 28/10/2015, se encuentra en la versión 4.1.2 (28/10/2015). Ocupa 134 MB.

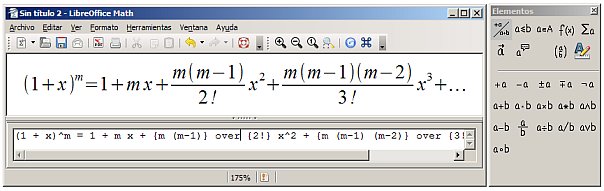
A través del menú Ver podemos activar el panel flotante de Elementos y tener un acceso rápido a las funciones. Sin embargo, con un poco de práctica puede hacer directamente. Por ejemplo: si queremos escribir la fracción 4/5 (el 4 encima del 5), podemos escribirlo directamente 4 over 5, en vez de ir a la barra flotante, seleccionar las fracciones y el botón que nos interese.
Antes de nada, para escribir subíndices y
superíndices con LibreOffice, no es necesario recurrir a LibreOffice
Math: seleccionas el texto y si quieres que sea un superíndice utilizas
el atajo de teclado CTRL + MAY + P (pulsas simultáneamente las teclas
CONTROL MAYÚSCULAS y la P -el signo + no hay que pulsarlo-); para
un subíndice el atajo es CTRL + MAY + B. También puedes
conseguir el mismo efecto a través del Menú Formato
> Carácter > Pestaña: Posición (Superíndice
o Subíndice). Un poco mas largo, ¿no?. Una posibilidad más
rápida es agregar a la barra de herramientas los botones de Superíndice,
Subíndice
y ya puestos el de Símbolos. En mi barra de LibreOffice yo
he agregado los botones: de Fórmula, Subíndice,
Superíndice
y Símbolos (para poder escribir las letras griegas, por ejemplo).
ej. Bo= 1,2 · 10-9 T. Para indicar los
decimales yo empleo una coma , y para el producto
el punto · (tecla MAY + 3). Este
"punto" está un poco más arriba · que el punto normal
.
pues éste puede confundirse con el decimal.
|
|
| Algunas ideas para facilitar la escritura
de fórmulas científicas con LibreOffice.
No os olvidéis de que contáis también con la Ayuda de LibreOffice a través del Menú Ayuda > Ayuda de LibreOffice (o F1 directamente), seleccionando el menú desplegable de LibreOffice Math. |
| Para agrupar términos (por ejemplo en un numerador) se emplean las llaves { y }. No olvidemos que tras uno que abre { tendrá que haber uno que cierra } |
| Para escribir una fracción y que quede bien claro cual es el numerador y el denominador, emplearemos el término over. Como en el ejemplo anterior 4 over 5 |
| Si queremos señalar un espacio adicional (para separar) : ~
Para pasar a una línea nueva y escribir otra fórmula por ejemplo: newline Las llaves se emplean para agrupar, si queremos poner una llave como tal: \{ Para escribir un vector: vec. Ejemplo: vec x Yo suelo indicar los vectores unitarios con un "gorrito chino" (circunflejo). Se señala con widehat. Ejemplo vec r = 2 widehat i - 3 widehat j Si lo que queremos es colocar una raya encima (en vez de un vector), para indicar el valor medio, por ejemplo, utilizamos el término bar. Ejemplo: bar x Si queremos escribir un comentario a continuación de una fórmula (que no se visualizará), escribiremos %% . Por ejemplo: y' + p (x) y = q (x) %% Ecuación diferencial lineal |
| Las letras griegas se escriben anteponiendo el símbolo
de tanto por ciento %:
Y para obtener la correspondiente mayúscula griega, pues se escribe en mayúscula. Por ejemplo: gamma (minúscula): %gamma ; gamma (mayúscula): %GAMMA Aquí van alguna de las letras griegas (minúsculas): alfa (minúscula): %alfa ; beta: %beta ; gamma (minúscula): %gamma ; épsilon: %epsilón ; mu: %my ; nu: %ny ; pi: %pi ; ro: %rho ; sigma (minúscula): %sigma ; ; sigma (mayúscula), o sea, el sumatorio: %SIGMA ; tau: %tau ; theta: %theta, etc. Sería muy útil aprender las más usuales. ¡ Atención para Apache OpenOffice: %mi (es la mu) ; %zeta (es theta) ; %ro (es ro) ! Puedes consultar todo el alfabeto griego en la parte inferior de la página. |
| Más símbolos...
pertenece: in. Ejemplo: a in b no pertenece: notint. Ejemplo: a notin b para todo: forall. Por ejemplo: forall vec x, vec y in %omega, vec x + vec y in %omega fecha a la derecha: rightarrow infinito: infinity menor o igual: leslant ó <= . Por ejemplo, x leslant 5 o x <=5 producirían el mismo resultado. mayor o igual: geslant ó >= . Por ejemplo, x geslant 5 o x >= 5 producirían el mismo resultado. distinto: <> aproximadamente igual: simeq implica: drarrow perpendicular (ortogonal): ortho. Por ejemplo: vec a ortho vec b paralelo: parallel. Por ejemplo: vec a parallel vec b equivalente (para un límite por ejemplo): sim o "~" (hay que entrecomillarlo). Por ejemplo: a sim b o bien a "~" b si queremos colocar un círculo sobre una letra usamos circle. Por ejemplo si queremos escribir la unidad del ämstrong: circle {nitalic A} un punto sobre una letra (para indicar por ejemplo la derivada) dot. Ejemplo: v = dot x dos puntos sobre una letra (para indicar por ejemplo la segunda derivada) ddot. Ejemplo: a = ddot x |
| Conjuntos: números naturales, enteros, reales, complejos, etc. Se antepone el término set. Ejemplo, para indicar el cuerpo de los números reales setN |
| Para indicar subíndices se emplea el sub, o el guión bajo_, por ejemplo B sub o B_o producen el mismo resultado |
| Para indicar potencias se emplea el sup o el ^. Por ejemplo: a sup 2 y a^2 producen el mismo resultado |
| Subíndices y superíndices a la izquierda lsub y lsup. Ejemplo: 1 n lsub 0 lsup 1 |
| Raíz cuadrada: SQRT . Ejemplo: SQRT 2 |
| Raíz de índice n: nroot {índice}. Ejemplo: nroot{3}{50/%pi} |
| Veamos un ejemplo de todo lo anterior:
%epsilón = {B sub o} over %tau func e^{-{t/%tau}} %pi a^2 cos(%theta) 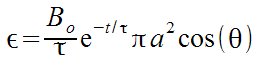 |
| Producto escalar cdot y vectorial times |
| vec a cdot vec b <> vec a times vec b
|
| Límites. Para indicar a que valor tiende la variable se emplea from y para la fecha rightarrow o %tiendea. No olvidar las llaves para agrupar los términos, numeradores, denominadores, etc. |
lim from{x rightarrow infinity}{{x^2-1} over
{x^2+1}}=1
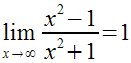 |
| lim from {x rightarrow 0} {{func e^{x} sin(x)
- x - x^2 } over {x^2 + x ln(1-x)} } = -{2 over 3}
lim from {x %tiendea 0} {{func e^{x} sin(x) - x - x^2 } over {x^2 + x ln(1-x)} } = -{2 over 3} 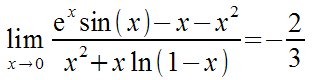 |
| Derivada. |
| d over {d x}left ({1 over {1+x^2}} right)= {-2x} over {1+x^2} |
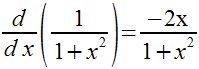 |
| Derivada parcial: partial |
| {partial (x^2+y^3)} over {partial x} = 2 x |
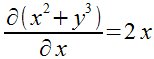 |
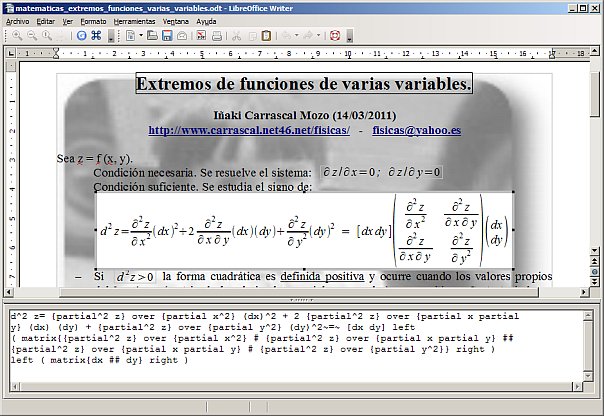
d^2 z= {partial^2 z} over {partial x^2} (dx)^2
+ 2 {partial^2 z} over {partial x partial y} (dx) (dy) + {partial^2 z}
over {partial y^2} (dy)^2
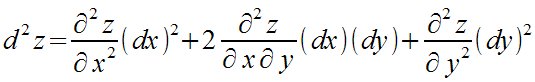 |
| Integral indefinida. |
| int from {} to {} {sin (x)} nitalic{d}x
= - cos (x) + C
o al no tener límites de integración: int {sin (x)} nitalic{d}x = - cos (x) + C |
|
|
| Integral definida. Para señalar la integral (sencilla) int, el límite inferior con from o la barra baja_ (antes del límite) y el límite superior con to o con ^(antes del límite) |
| Integral: int ; Integral doble: iint; Integral triple: iiint |
| Integral curvilínea cerrada: lint ; Integral doble (cerrada): llint; Integral triple (cerrada): lllint |
| int from {0} to {1} {x^2} nitalic{d}x = 1 over 3 |
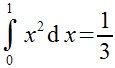 |
| P ( X leslant x)= int from - infinity to x {f
(x) dx} = F (x)
P ( X leslant x)= int _{- infinity} ^x {f (x) dx} = F (x) 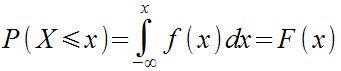 |
lint from {C} to {} {(2 x y - x^2) dx +
(x + y^2) dy}
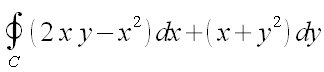 |
| Matrices. Con el término matrix, separando los elementos en una fila por almohadillas # y de una fila a otra con almohadillas dobles ## |
| Para indicar un paréntesis de tamaño "ajustable a lo
que haya detrás", empleamos el left ( para el paréntesis
izquierdo y el right ) para el derecho. Si no quisieramos colocar
el paréntesis derecho, escribiríamos: right
none
Determinanantes. En lugar de paréntesis left ( y right ) utilizaremos líneas verticales left lline y right lline Si queremos colocar corchetes ajustable en vez de paréntesis o líneas verticales, usamos left [ y right ] |
[dx dy] left ( matrix{{partial^2 z} over {partial
x^2} # {partial^2 z} over {partial x partial y} ## {partial^2 z} over {partial
x partial y} # {partial^2 z} over {partial y^2}} right ) left ( matrix{dx
## dy} right )
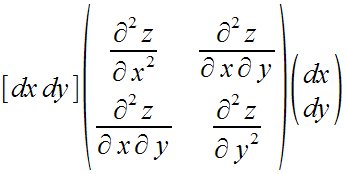 |
| Para señalar la típica función que toma diferentes valores en varios intervalos, colocamos una llave a la izquierda (pero no a la derecha) left lbrace y right none |
f (x) = left lbrace matrix{{a x ~ para ~ 0<x<1}
## {0 ~ para ~ x notin (0,1)}} right none
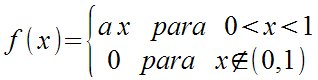 |
| Sistemas de ecuaciones. |
alignl left lbrace stack{{{ x+y+z} = {6} } `#`
{ {{2}x-y+{3}z} = {9} } `#` { {{3}x+{2}y-z} = {4} }} right none
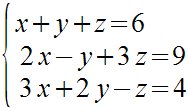 |
| Si queremos que algún símbolo no sea interpretado, por
ejemplo, quiero escribir una llave { lo que hacemos es entrecomillarla:
"{"
vec nabla vec E = "div" {vec E} = %rho over %epsilón sub o 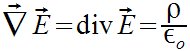 |
| El tamaño. En ocasiones el símbolo "por defecto" se nos
queda un poco pequeño. Por ejemplo, si queremos hacer una integral
con un integrando un poco más complicado, podemos emplear la palabra
size.
Por ejemplo si escribimos la integral definida siguiente: int from {1} to {2} {{1 over x} over {1 over SQRT x + SQRT x over x}} nitalic{d}x 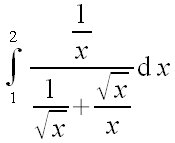 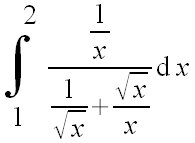 |
|
|
| Matemáticas > Un sumatorio
sum from {k=1} to {n} {k^{2}} = {( (n+1-3/2 )(n+1) + 1/2 ) (n+1)} over 3 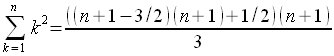 |
| Matemáticas > Un productorio
prod from {k=1} to {n} {k^2} = 1 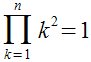 |
| Matemáticas > Producto de matrices
left( matrix{{1}`#{2}`#{3}`##{4}`#{5}`#{6}} right)· left( matrix{{1}`#{2}`##{3}`#{4}`##{5}`#{6}} right) = left( matrix{{22}`#{28}`##{49}`#{64}} right) 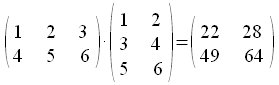 |
| Matemáticas > Un límite por la izquierda y otro por
la derecha
lim from{x rightarrow {0}^-{}}{1 over x} = - infinity 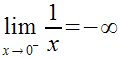 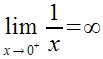 |
| Matemáticas > Un límite
Vamos a calcular un límite en el que aparece una integral y tengamos que aplicar la regla de L´Hôpital, el teorema fundamental del cálculo integral y equivalencias para llegar al resultado.. lim from {x %tiendea 0} {{int from 0 to 2x sin (t^2) dt} over {x^3}} ~=~ lim from {x %tiendea 0} {{sin (2x)^2 cdot 2} over{3x^2}} ~=~ {2 over 3} lim from {x %tiendea 0} {{sin (4x^2)} over {x^2}} ~sim~ {2 over 3} lim from {x %tiendea 0}{{4 overstrike {x^2}}over {overstrike {x^2}}}~=~ 8 over 3 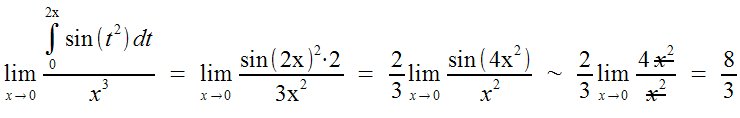 |
| Física > Centro de masas de una barra uniforme
x sub {CM} = { int {x} d m } over { int {} d m } = { int from {0} to {L} {x} %lambda d x } over M = {left [%lambda x^2 over 2 right ]sub 0 ^L} over M = {%lambda L^2 over 2} over M = {%lambda L^2 over 2} over {%lambda L} = L over 2 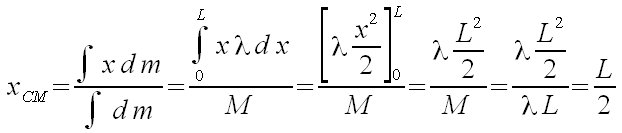 |
| Matemáticas / Física > Producto mixto de tres vectores
vec a cdot (vec b times vec c) = left lline matrix{a sub x`#a sub y`#a sub z`##b sub x`#b sub y`#b sub z`##c sub x`#c sub y`#c sub z} right rline 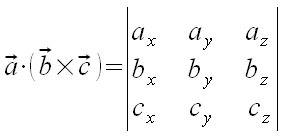 |
| Matemáticas > Series numéricas. Criterio de Raabe
"Si " lim from {n %tiendea infinity} left [n left ( 1 - {a sub {n+1}} over {a sub n} right) right] ~> ~1 drarrow " converge" 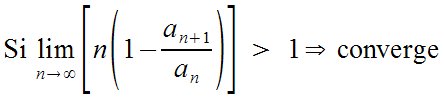 |
| Matemáticas / Física > Gradiente de una función
escalar
vec NABLA %fi = {partial %fi} over {partial x} vec i + {partial %fi} over {partial y} vec j + {partial %fi} over {partial z} vec k 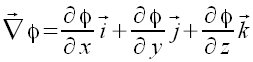 |
| Matemáticas / Física > Divergencia de un vector
"div" {vec A} = vec NABLA vec A = {partial A sub x} over {partial x} + {partial A sub y} over {partial y} + {partial A sub z} over {partial z} 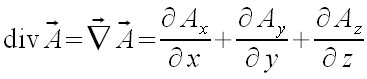 |
| Matemáticas / Física. Rotacional de un vector.
rot vec A = vec nabla times vec A = left lline matrix{vec i`#vec j`#vec k`##partial over {partial x}`#partial over {partial y}`#partial over {partial z}`##A sub x`#A sub y`#A sub z} right rline^{} 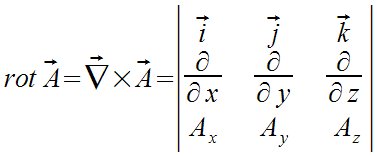 |
| Matemáticas / Física. Rotacional de un vector F (expresión
desarrollada)
rot vec F = left ( {partial F sub z} over {partial y}- {partial F sub y} over {partial z} right ) vec i + left ( {partial F sub x} over {partial z}- {partial F sub z} over {partial x} right ) vec i + left ( {partial F sub y} over {partial x}- {partial F sub x} over {partial y} right ) vec i 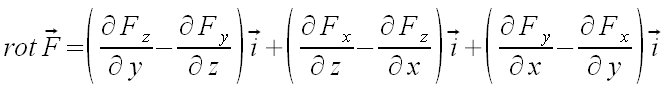 |
| Matemáticas / Física > Laplaciano en coordenadas polares
nabla^2 u = {partial ^2 u} over {partial %rho ^2} + {1 over %rho} {partial u} over {partial %rho} + {1 over {%rho ^2}} {partial ^2 u} over {partial %theta ^2} 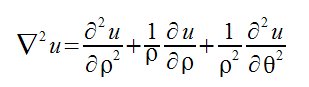 |
| Matemáticas / Física > Laplaciano en coordenadas esféricas
NABLA^2 %PSI = {partial^2 %PSI} over {partial r^2} + 2 over r {partial %PSI} over {partial r} + {ctg %PSI} over {r^2} {partial %PSI} over {partial %theta} + 1 over {r^2} {partial^2 %PSI} over {partial %theta^2} + 1 over {r^2 sin %theta} {partial^2 %PSI} over {partial %fi^2} 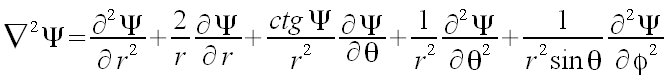 |
| Matemáticas > Plano tangente a una superficie en un punto
de la misma si la superficie viene dada en forma explícita
left ( {partial z} over {partial x} right) sub P (x - x sub o) + left ( {partial z} over {partial y} right) sub P (y - y sub o) = z - z sub o 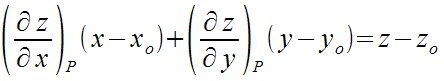 |
| Matemáticas > Desarrollo en serie de Taylor hasta grado cinco
de la función sin (x) en torno al origen.
sin x = x - x^3 over {3 nitalic!} + x^5 over {5 nitalic !} 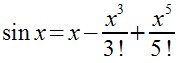 |
| Matemáticas > Desarrollo en serie de una función de
varias variables
f (x,y) = f (x sub o,y sub o) + {1 over {1!}} left[ { {partial f} over {partial x} (x sub o,y sub o) } (x - x sub o) + { {partial f} over {partial y} (x sub o,y sub o) } (y - y sub o) right ] newline + {1 over {2!}} left[ { {partial^2 f} over {partial x^2} (x sub o,y sub o) } (x - x sub o)^2 + 2 { {partial^2 f} over {partial x partial y} (x sub o,y sub o) } (x - x sub o)(y - y sub o)+ { {partial^2 f} over {partial y^2} (x sub o,y sub o) } (y - y sub o)^2 right ] + ... 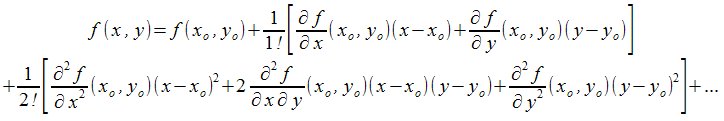 |
| Matemáticas > Wronsquiano
W (x) = left lline matrix{f sub {1}`#f sub {2}`#f sub {3}`##{f' sub {1}} `#{ f' sub {2}} `#{f' sub {3}} `##f'' sub {1}`#f'' sub {2}`#f'' sub {3}} right rline 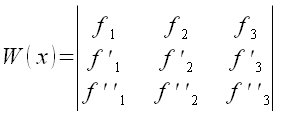 |
| Matemáticas > Jacobiano
{D (u,v,%omega)} over {D (x,y,z)} = left lline matrix{{partial u} over {partial x}`#{partial u} over {partial y}`#{partial u} over {partial z}`##{partial v} over {partial x}`#{partial v} over {partial y}`#{partial v} over {partial z}`##{partial %omega} over {partial x}`#{partial %omega} over {partial y}`#{partial %omega} over {partial z}} right rline 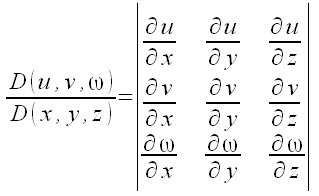 |
| Matemáticas > Hessiano
H (x, y ) = left lline matrix{{partial^2 z} over {partial x^2} # {partial^2 z} over {partial x partial y} ## {partial^2 z} over {partial x partial y} # {partial^2 z} over {partial y^2}} right rline 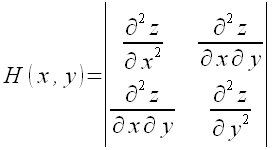 |
| Matemáticas > Integrales trigonométricas. Sustitución
general. Cuando el integrando es una función par en sin x y
cos x, se hace el cambio
tan x = t ~drarrow ~sin x = t over SQRT{1+t^2} ~;~ cos x = 1 over SQRT {1+t^2}~;~ dx = {dt} over {1+t^2} 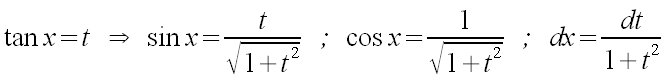 |
| Matemáticas > Integrales irracionales
size *2 int size *0.5 {R left( x, left({ax+b} over {cx+d} right)^ left(m over n right), left({ax+b} over {cx+d} right)^ left(p over q right), dotslow , left({ax+b} over {cx+d} right)^ left(r over s right) right) dx} 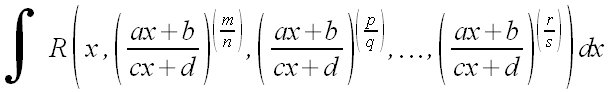 |
| Matemáticas > Teorema fundamental del cálculo integral
d over {dx} left [ int from {u (x)} to {v (x)} {f (t)} nitalic{d}t right ]= f ( v(x)) v' (x) - f(u(x)) u' (x) 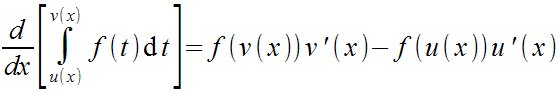 |
| Matemáticas > Ecuaciones diferenciales
left lbrace stack{{ {y-xy'} = {{3}({1}+x^{2} y')} } `#` { {y ({1})} = {4} }} right none 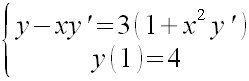 |
| Matemáticas > Una transformada de Laplace
L (t^2)= int from {0} to {infinity} {t^2 e^{- s t}} d t = 2 over {s^3} 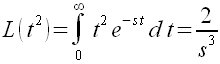 |
| Matemáticas > Métodos numéricos > Método
iterativo de Gauss - Seidel
x sub {nitalic i} ^(r+1) = { b sub {nitalic i} - sum from {{nitalic j}={1}} to {{nitalic i}-{1}} {a sub {ij} · x sub {nitalic j} ^(r+1)} - sum from {{nitalic j}={nitalic i}+{1}} to {n} {a sub {ij} · x sub {nitalic j} ^{(r)}} } over a sub {ii} 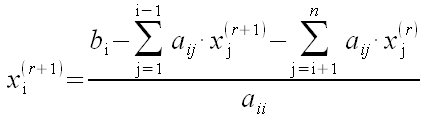 |
| Matemáticas > Desviación típica
%sigma = SQRT{{{sum x sub {nitalic i} ^{2}} over N}- {bar x}^{2}} 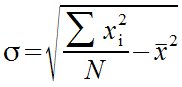 |
| Matemáticas > Covarianza
%sigma sub {xy} = {sum ({x sub {nitalic i} y sub {nitalic i}}) over N}- {bar x} {bar y} 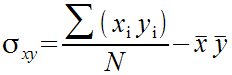 |
| Matemáticas > Función de distribución normal.
f (x) = 1 over {%sigma SQRT {2 %pi}}func e^{-{1 over 2} left ({{x - %my}over %sigma}right )^2} 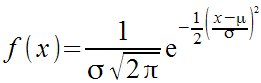 |
| Física > Cinemática > Movimiento relativo: vector
aceleración
vec a = vec A + vec %alfa times vec r´ + vec %omega times (vec %omega times vec r´) + 2 vec %omega times vec v´ + vec a´ |
| Física > Mecánica analítica. La solución
para encontrar el extremal de la integral siguiente nos lo da la ecuación
de Euler
int from {x sub 1} to {x sub 2} f ( y (x), y' (x), x) dx 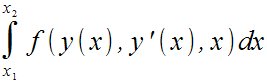 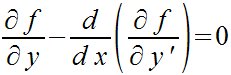 |
| Física > Teorema de Gauss
llint vec E cdot d vec S ={q sub neta} over {%epsilón sub o} 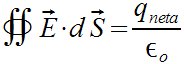 |
| Física > Ley de Biot y Savart
d vec B= {%my sub o I} over {4 %pi} {d vec l times vec r} over r^3 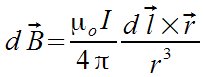 |
| Física > Ley de Ampère
lint vec B cdot vec {dl} = %my sub 0 I sub{enc} |
| Física Nuclear. Una reacción nuclear (empleamos
el ~ para separar un poco los elementos entre sí)
U lsub 92 lsup 235 ~+~ n lsub 0 lsup 1 ~rightarrow~ Sr lsub 38 lsup 95 ~+~ Xe lsub 54 lsup 139 ~+~ 2 n lsub 0 lsup 1 |
| Física Cuántica > Ecuación de Schrödinger
dependiente del tiempo
-{hbar^2 over {2m}}{partial^2 %PSI (x, t)} over { partial x^2} ~+~ V (x) %PSI (x, t) ~=~ i hbar {%PSI (x, t)} over {partial t} 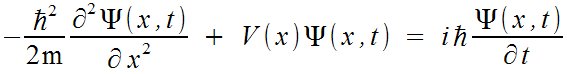 |
| Física Cuántica > Ecuación de Schrödinger
independiente del tiempo
-{hbar^2 over {2m}}{d^2 %PHI (x)} over { d x^2} ~+~ V (x) %PHI (x) ~=~ E %PHI(x) 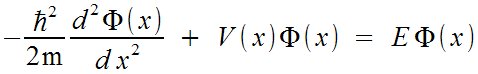 |
| Física Cuántica > Una integral definida útil
int from {0} to {infinity } {x^{{2}n} {nitalic e}^{-a x^{2}}} nitalic{d}x = {{1} · {3} · {5} dotslow ·({2}n-{1})} over {{2}^{n+{1}} a^n} SQRT {%pi over a} 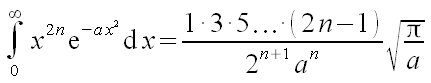 |
| Vamos a resolver un problema de electromagnetismo.
Calcular la inductancia mutua entre un hilo largo por el que circula una corriente I1 y una espira rectangular de dimensiones a y b con el lado a paralelo al hilo largo y a una distancia c del mismo. "Campo magnético creado por una corriente rectilínea infinita:" B sub 1 = {%my sub o I sub 1} over {2 %pi r} newline "Flujo que la corriente rectilínea crea sobre la espira rectangular:" newline %PHI sub{12} = iint {vec {B sub 1} cdot vec {ds}} = int from c to {c+b} {{%my sub o I sub 1} over {2 %pi r} a dr} = {%my sub o a I sub 1} over {2 %pi} ln left ({c+b} over c right) newline "Coeficiente de inducción mutua entre la corriente y la espira:" newline M = {%PHI sub {12}} over {I sub 1} = {%my sub o a} over {2 %pi} ln left ({c+b} over c right)  |
| Química > Constante de equilibrio de una reacción:
"La constante de equilibrio de la reacción " Br sub 2 + H sub 2 rightarrow 2 Br H " es:" newline K sub c = [Br H]^2 over {[Br sub 2] [H sub 2]} 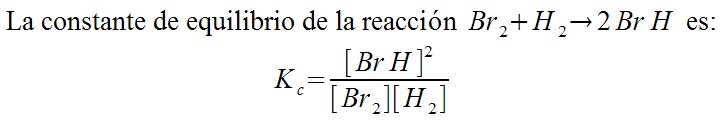 |
| Química > Variación de entalpía de una reacción:
%DELTA H = sum H ^o _f (productos) - sum H ^o _f (reactivos) |
|
|
Las letras griegas se escriben anteponiendo
el símbolo de tanto por ciento %:
Y para obtener la correspondiente mayúscula
griega, pues se escribe en mayúscula. Por ejemplo: gamma (minúscula):
%gamma
; gamma (mayúscula): %GAMMA
Hay algunas diferencias en cómo se escriben
dichas letras griegas en LibreOffice y en Apache OpenOffice. ¿Qué
letras cambian? : epsilon, theta, upsilon (por la situación de los
acentos); mu, omicron, rho, chi, zeta, kappa (tanto en las mayúsculas
como en las minúsculas).
|
|
||||||||||||||
| Alpha | A |
|
a |
|
Iota | I |
|
i |
|
Rho | R |
|
r |
|
| Beta | B |
|
b |
|
Kappa | K |
|
k |
|
Sigma | S |
|
s |
|
| Gamma | G |
|
g |
|
Lambda | L |
|
l |
|
Tau | T |
|
t |
|
| Delta | D |
|
d |
|
Mu | M |
|
m |
|
Upsilon |
|
|
||
| Epsilon | E |
|
e |
|
Nu | N |
|
n |
|
Phi | F |
|
f |
|
| Zeta | Z |
|
z |
|
Xi |
|
|
Chi |
|
|
||||
| Eta | H |
|
h |
|
Omicron |
|
|
Psi | Y |
|
y |
|
||
| Theta | Q |
|
q |
|
Pi | P |
|
p |
|
Omega | W |
|
w |
|
|
|
||||||||||||||
|
|
||||||||||||||
| Alpha | A |
|
a |
|
Iota | I |
|
i |
|
Rho | R |
|
r |
|
| Beta | B |
|
b |
|
Kappa | K |
|
k |
|
Sigma | S |
|
s |
|
| Gamma | G |
|
g |
|
Lambda | L |
|
l |
|
Tau | T |
|
t |
|
| Delta | D |
|
d |
|
Mu | M |
|
m |
|
Upsilon |
|
|
||
| Epsilon | E |
|
e |
|
Nu | N |
|
n |
|
Phi | F |
|
f |
|
| Zeta | Z |
|
z |
|
Xi |
|
|
Chi |
|
|
||||
| Eta | H |
|
h |
|
Omicron |
|
|
Psi | Y |
|
y |
|
||
| Theta | Q |
|
q |
|
Pi | P |
|
p |
|
Omega | W |
|
w |
|
|
|
||||||||||||||
|
|
Dmaths.org. es una extensión (añade
varias barras de herramientas) que nos va a ayudar en nuestra tarea de
escribir fórmulas rápidamente.
¿Dónde conseguirlo? En
la página oficial (en francés): http://www.dmaths.org/
En inglés: http://www.dmaths.org/documentation/doku.php?id=presentation:en
La última versión (revisada el 16/11/2014)
es la 3.5.2.5 y el archivo ocupa 15,4 MB. Además está en
castellano.
A continuación un detalle de la barra de herramientas que incorpora Dmaths:
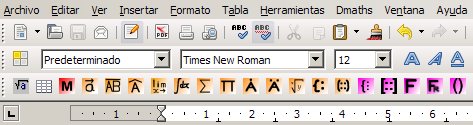
Podremos escribir fórmulas, recuadrarlas, vectores, sistemas de ecuaciones, límites, integrales, sumatorios, etc. Facilita enormente la introducción de fórmulas, sistemas de ecuaciones, matrices, integrales, límites, etc.
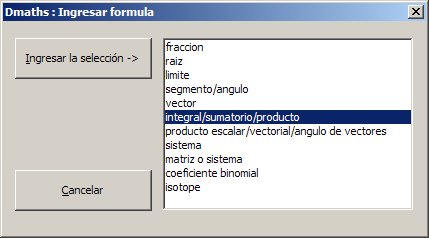
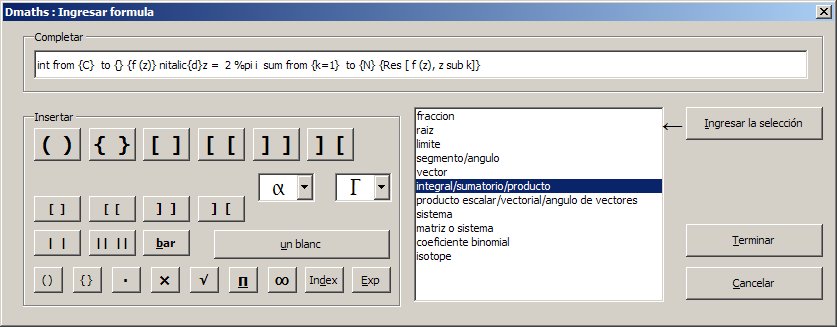
Ingreso de una fórmula "complicada" con Dmaths
Puedes escribir directamente la fórmula en el procesador de textos LibreOffice Writer en el formato LibreOffice Math, la seleccionas (con el ratón o con el teclado) y al pulsar F10 te escribe directamente la fórmula.
Yo suelo emplear el método anterior en la mayoría de las ocasiones (escribir la fórmula directamente en LibreOffice Writer, seleccionarla y pulsar F10). Para fórmulas más complicadas, matrices, sistemas, integrales, sumatorios... empleo el Asistente para fórmulas o el Asistente extendido para fórmulas de Dmaths. También empleo el Cuadro de fórmula, para recuadrar una fórmula.
Dmaths incluye además otras herramientas que
permiten hacer gráficas, ajuste de curvas no lineales (Non linear
curve fitting 1.2, Laurent Godard, mayo 2004), o figuras geométricas
(en dos y tres dimensiones), por ejemplo.
|
|
| Jueves 12 de abril de 2012 23:31 | DE: Sebastian Agrelo |
| Excelente aporte!!!!
Mil gracias. Salu2. |
|
| Lunes, 14 de enero de 2013 | DE: Guillermo Molleda Jimena |
| Buenos días:
Magnífica página la que explica esto de las fórmulas
con LibreOffice:
|
|
| mié, 3 abr 2013 a las 4:44 | DE: Raul Ascencio |
| Muchas gracias.
http://www.carrascal.net46.net/fisicas/informatica/libreoffice_math.htm |
|
| mar 25 a las 11:20 PM | DE: pablo ortiz |
| Muy buena la página! muy útil y bien explicado, las fórmulas con ejemplos van genial. Saludos! | |
| sáb 29 a las 4:20 PM | DE: Salva Open-Office Es |
| Hola Mari Paz e Iñaki
Encontré por casualidad vuestras páginas, y me han impresionado. Me he permitido la libertad de mencionaros en el blog (http://blog.open-office.es/index.php/math/2014/03/29/pagina-con-ejemplos-de-openoffice-y-libreoffice-math) y en la wiki (http://wiki.open-office.es/Recursos_Math) |
|
|
https://nuestrospueblos.000webhostapp.com/fisicas/ - https://kddj.000webhostapp.com/fisicas/ ) Dirección actual: https://castrillodedonjuan.com/fisicas/ Desde mi blog se puede acceder a la última dirección disponible: http://matematicasfisicaquimicauva.blogspot.com/ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|